Order of Operations
Grade 6 Math Worksheets
In every walk of life, we are met with a set of orders or patterns without which everything falls apart.
Just like when we get up in the morning we brush our teeth, finish our morning ablutions, eat breakfast, pack our stuff, and leave for school.
We cannot afford to mess up the order because then it gets absurd.
In the same way in Mathematics, a principle for order of operations is followed.
‘Operations’ means to add, subtract, multiply, divide, square, etc. If it isn’t a number it is probably an operation.
But if we came across – 3 + (8 × 32 + 9), How should we calculate?
- Will a left-to-right solution get us the answer?
- Will a right-to-left lead to the right answer?
- Will solving the exponents first and then the rest get us to the end?
All across the globe mathematicians were completely confused with the respective results.
Hence, they came up with a conclusion to follow an order to operate a set of parameters.
Personalized Online Tutoring
Order of Operations - Grade 6 Math Worksheet PDF
This is a free printable / downloadable PDF worksheet with practice problems and answers. You can also work on it online.
Sign up with your email ID to access this free worksheet.
"We really love eTutorWorld!"
"We really love etutorworld!. Anand S and Pooja are excellent math teachers and are quick to respond with requests to tutor on any math topic!" - Kieran Y (via TrustSpot.io)
"My daughter gets distracted easily"
"My daughter gets distracted very easily and Ms. Medini and other teachers were patient with her and redirected her back to the courses.
With the help of Etutorworld, my daughter has been now selected in the Gifted and Talented Program for the school district"
- Nivea Sharma (via TrustSpot.io)
Order of Operations in Math
The order of operations is the order that is followed to add, subtract, multiply, or divide to solve a problem in mathematics.
Order of operations is the method by which operations should be performed in a particular order. It gives us a procedure as to which operations to do first.
Order of Operations Definition
The order of operations is a fundamental principle in mathematics used to standardize the sequence of steps to solve mathematical expressions.
It outlines a hierarchy of operations to be followed when multiple operations are present in an expression.
These guidelines are established by assigning operators a rank known as precedence, determining the order in which operations are executed. Operations with higher precedence take priority over those with lower precedence, ensuring a specific sequence in solving mathematical expressions.
The commonly accepted order is parentheses, exponents, multiplication and division (from left to right), and addition and subtraction (from left to right).
Following this order ensures that everyone arrives at the same result when evaluating an expression, preventing ambiguity and ensuring accuracy in mathematical calculations. This fundamental principle is crucial in maintaining consistency and precision across mathematical computations and problem-solving scenarios.
Solving the Puzzle: Order of Operations Rules
These rules, often remembered by acronyms like PEMDAS, help us solve expressions correctly, step by step.
PEMDAS rule is pivotal in systematically tackling complex mathematical equations.
Imagine you have a tricky math problem—a puzzle waiting to be solved. These rules act as your trusty guide through the maze of numbers and operations, ensuring you follow the right path.
Rule 1: Parentheses/Brackets First
The journey begins by looking inside the parentheses or brackets. It is like solving secrets within hidden boxes! We solve what is inside these first, moving from the inside out, following the order of parentheses: round brackets first, then curly brackets, and finally, box brackets.
Rule 2: Exponents Next
Next stop: Exponents!
These are like the magical powers of numbers, making them grow or shrink specially. We solve any exponent problems we find after solving the parentheses.
Rule 3: Multiplication & Division Turn
Now, it is time for Multiplication and Division.
Like taking steps on a path, we solve these operations as we approach them, moving from left to right in the expression.
Rule 4: Addition & Subtraction Wrap-up
Finally, we reached the last part of our journey: Addition and Subtraction. Similar to the final steps in a journey, we solve these from left to right, too.
Understanding and following these rules ensures that we solve math problems correctly. They are like a secret code to unlock the correct answers, making math adventures easier and more fun!
Way to Remember Order of Operations
To remember the conventional order of operations, you can think of –
PEMDAS (Remember the phrase – ‘Please excuse my dear Aunt Sally’ or ‘Please Eat My Delicious Apple Slices’ to memorize this easily)
P – Parentheses
E – Exponents
M D – Multiplication and Division
A S – Addition and Subtraction
BODMAS follows a similar order, starting with brackets, handling orders or exponents next, then proceeding to division, multiplication, addition, and subtraction.
These acronyms provide a systematic way to remember the order of operations, ensuring that mathematical expressions are solved correctly by following a specific hierarchy:
- Addressing brackets or parentheses
- Handling exponents
- Performing multiplication/division
- Executing addition/subtraction in a defined sequence for accurate results
Now see the difference between a Random Method to solve an expression and the PEDMAS Method.
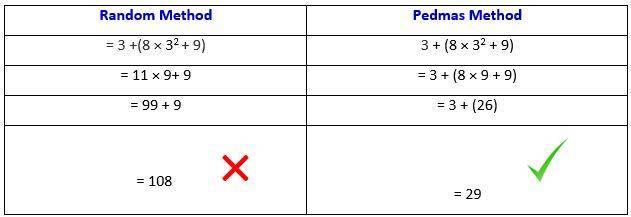
“There have been times when we booked them last minute, but the teachers have been extremely well-prepared and the help desk at etutorworld is very prompt.
Our kid is doing much better with a higher score.”
6th Grade Tutoring
eTutorWorld offers Personalized Online Tutoring for Math, Science, English, and Standardised Tests.
Our Tutoring Packs start at just under $22.49 per hour, and come with a moneyback guarantee.
Schedule a FREE Trial Session, and experience quality tutoring for yourself. (No credit card required.)
PEMDAS vs BODMAS
Mathematical operations involve a systematic approach to solving complex equations.
Two commonly used acronyms, PEMDAS and BODMAS, delineate the sequence of operations for solving mathematical expressions.
Origins of PEMDAS and BODMAS
PEMDAS, commonly used in the United States and Canada, stands for Parentheses, Exponents, Multiplication, Division (from left to right), Addition, and Subtraction (from left to right).
This acronym succinctly outlines the hierarchy of operations to be followed when solving equations.
On the other hand, BODMAS, prevalent in the United Kingdom, India, and some other countries, represents Brackets, Orders (powers and square roots, etc.), Division and Multiplication (from left to right), Addition and Subtraction (from left to right).
PEMDAS and BODMAS lay down rules to avoid ambiguity in mathematical computations, ensuring a standardized approach to solving equations.
Application and Variations
While PEMDAS and BODMAS share the fundamental principles of the order of operations, minor variations exist in their terminology.
For instance, PEMDAS uses ‘Parentheses’ while BODMAS refers to ‘Brackets.’
Similarly, ‘Exponents’ in PEMDAS equate to ‘Orders’ in BODMAS, signifying powers or square roots.
How to Use Order of Operations?
Examining the following examples allows us to grasp the precision with which the rules of order of operations have been applied, aiding our understanding of their accuracy.
Example 1
6+3×2
Here, we use PEMDAS:
Multiplication comes before addition, so we solve 3×2 first.
Therefore,
6+6=12.
Answer: 12
Example 2
4+5×(6−2)
Here, we encounter parentheses/brackets:
Solve inside the parentheses/brackets first: 6−2=4
Now, we have 4+5×4
Multiply before addition: 5×4=20, then 4+20=24
Answer: 24
Example 3
(8−3)^2÷5
Here, we have both parentheses/brackets and an exponent/order:
Solve inside the parentheses/brackets first: 8−3=5
Now, we have 5^2÷5
Exponent/order comes before division: 5^2=25, then 25÷5=5.
Answer: 5
These examples demonstrate that correctly following the order of operations (PEMDAS) leads to accurately evaluating mathematical expressions.
Improper sequencing can result in vastly different and often incorrect answers.
Real-Life Applications of Order of Operations
The order of operations is genuinely used in various everyday situations. Let us explore another common scenario where this concept comes into play:
Scenario
You are organizing a school event and need to distribute snacks equally among a certain number of students. You have bought 8 packs of cookies, each containing 12 cookies. You want to know how many cookies each student will get.
Given:
Total packs of cookies = 8
Cookies per pack = 12
Total students = 24
Expression using PEMDAS
Expression: (8×12)/24
Solution
1. Multiplication
First, solve the number of total cookies by multiplying the packs by the cookies per pack.
8×12=96 in total
2. Division
Now divide the total number of cookies by the number of students to distribute them equally.
96/24=4
Conclusion
In this case, each student will receive 4 cookies using the order of operations.
It illustrates how the order of operations helps determine fair distribution, ensuring everyone gets an equal share of snacks during events or gatherings.
This scenario showcases how the order of operations guides us in organizing and dividing resources evenly, making it easier to manage group activities or events reasonably and efficiently.
Whether it is cookies, pizzas, or any other items to be distributed equally, understanding the order of operations ensures a fair and accurate distribution among individuals involved in various real-life situations.
Order of Operations Examples
Let’s work through a couple of word problems that involve applying the order of
operations to solve real-life scenarios.
Example 1
Scenario: Sara has 4 boxes, and each box contains 12 chocolates. She wants to share them equally among her 3 friends. How many chocolates will each friend receive?
Solution:
Given:
Number of boxes = 4
Chocolates per box = 12
Number of friends = 3
Expression: (4×12)÷3
- Multiplication: Calculate the total number of chocolates.
- 4×12=48 chocolates in total.
- Division: Divide the total chocolates among the friends.
- 48÷3=16
Each friend will receive 16 chocolates.
Example 2
Scenario: Alex has $60. He spends $12 on a book and $18 on stationery and then divides the remaining money equally among his 4 siblings. How much money does each sibling receive?
Solution:
Given:
Total money = $60
Money spent on book = $12
Money spent on stationery = $18
Number of siblings = 4
Expression: (60−12−18)÷4
- Subtraction: Calculate the remaining money after spending on the book and stationery.
- 60−12−18=30 dollars remaining.
- Division: Divide the remaining money among the siblings.
- 30÷4=7.5
Each sibling will receive $7.50.
Example 3
Scenario: Emily has 24 cupcakes to distribute equally among 6 friends. Each friend wants 2 cupcakes for themselves, and the remaining cupcakes will be shared equally among Emily’s family members. How many cupcakes will each family member receive?
Solution:
Given:
Total cupcakes = 24
Number of friends = 6
Expression: (24−(6×2))÷Family members
- Multiplication: Calculate the number of cupcakes the friends take.
- 6×2=12 cupcakes for friends.
- Subtraction: Find the remaining cupcakes.
- 24−12=12 cupcakes remaining.
- Division: Distribute the remaining cupcakes among the family members.
- Let’s say there are 4 family members.
- 12÷4=3
Each family member will receive 3 cupcakes.
Example 4
Scenario: A garden has 30 flowerbeds. Each flowerbed contains 9 flowers. How many flowers remain in the garden if 5 flowerbeds are replanted, each with 12 flowers?
Solution:
Given:
Total flowerbeds = 30
Flowers per flowerbed = 9
Replanted flower beds = 5
Flowers in each replanted flower bed = 12
Expression: (30×9)−(5×12)
- Multiplication: Find the total number of flowers in the garden initially.
- 30×9=270 flowers initially.
- Multiplication: Calculate the total number of flowers replanted.
- 5×12=60 flowers replanted.
- Subtraction: Determine the remaining number of flowers.
- 270−60=210
210 flowers are remaining in the garden.
These examples demonstrate how the order of operations helps solve practical problems involving everyday situations, ensuring fair distributions or calculations are done accurately.
Check Point
Now try to answer the following
- 29 – 23 × 0 ÷ 1
- 65 ÷ 5 × 7 × 3
- 19 – 12 + 4 × 3
- 4 × 4 ÷ 1 + 9
- 20 – 10 × 3 ÷ 1
Answer key
- 0
- 273
- 19
- 25
- 30
Do You Stack Up Against the Best?
If you have 30 minutes, try our free diagnostics test and assess your skills.
Order of Operations FAQS
What is the Order of Operations, and why is it important?
The order of operations is a set of rules that tells us the sequence in which we solve math problems involving multiple operations like addition, subtraction, multiplication, and division. It is important because it ensures everyone gets the same answer when solving the same problem.
What does 'PEMDAS' stand for?
PEMDAS is a helpful acronym to remember the order of operations. It stands for parentheses, extensions, multiplication and division (from left to right), and addition and subtraction (from left to right).
Why do we need to follow the order of operations?
Following the order of operations is like having a rulebook for math. It helps us solve problems step-by-step in a fair and organized way so that everyone gets the correct answer.
Can you give an example of using the order of operations in real life?
Sure! Imagine you have to solve a math problem involving buying snacks for friends. You need to know how much each friend should pay. Following the order of operations, you can figure out the total cost and divide it equally among friends to be fair.
How do brackets and parentheses fit into the order of operations?
Brackets and parentheses show us which parts of a math problem to solve first. We start by solving what is inside them before moving to other operations.
Can the order of operations change the answer?
Yes! If we do not correctly follow the order of operations, we might get a different answer. It is like following a recipe—doing things in the wrong order might change the taste of the food!
Why can't we just solve problems from left to right?
Sometimes, if we only solve problems from left to right without following the order of operations, we might get the wrong answer. The order of operations helps us solve problems correctly.
How can I remember the order of operations better?
You can use tricks like PEMDAS or make up your fun phrase to remember the order: ‘Please Excuse My Dear Aunt Sally’ or ‘Please Eat My Delicious Apple Slices.’
Can the order of operations help solve problems in video games or building things?
Absolutely! Math is everywhere. Whether playing games, building structures, or even planning your time, understanding the order of operations can help you think and solve problems better.
Is there an easy way to check if I have solved a problem using the order of operations correctly?
Yes! After solving a problem, check your work by asking your teacher or using a calculator. It is like double-checking your work to make sure everything is correct.

Gloria Mathew writes on math topics for K-12. A trained writer and communicator, she makes math accessible and understandable to students at all levels. Her ability to explain complex math concepts with easy to understand examples helps students master math. LinkedIn
Affordable Tutoring Now Starts at Just $22.49
eTutorWorld offers affordable one-on-one live tutoring over the web for Grades K-12. We are also a leading provider of Test Prep help for Standardized Tests (SCAT, CogAT, MAP, SSAT, SAT, ACT, ISEE, and AP).
What makes eTutorWorld stand apart are: flexibility in lesson scheduling, quality of hand-picked tutors, assignment of tutors based on academic counseling and diagnostic tests of each student, and our 100% money-back guarantee.
Whether you have never tried personalized online tutoring before or are looking for better tutors and flexibility at an affordable price point, schedule a FREE TRIAL Session with us today.
*There is no purchase obligation or credit card requirement
Grade 6 Science Worksheets
- Inquiry process
- Nature of Science
- Scientific Inquiry
- Inquiry, Analysis and Problem Solving
- Ethical Practices
- Science and Society
- Biotic and Abiotic Factors
- Impact of Organisms
- Adaptation
- Spheres of Earth
- Natural Resources
- Environmental Issues
- Conservation of Earth
- Understanding Technology
- Abilities To Do Technological Design
- Structure of Earth
- Solar System
- Rocks and Fossils
- Earth Systems
- Plate Tectonics
- Evolution
- Magnetic Field of Earth
- Geologic Time
- Materials and Processes That Shape a Planet
- Astronomy
- Ecology
- Energy
- Kinetic and Potential Energy
- Energy Transfer
- Matter and its Structure
- States of Matter
- Physical and Chemical Changes
- Force and Motion
- Electricity and Magnetism
- Wave Interactions
- Sound
- Light
- Introduction to Life Science
- The Origin & History of Life On Earth
- Plant and Animal Cells
- Parts of a Cell
- The Cell Cycle
- How Living Organisms Get Energy
- Classification of Organisms
- How Plants Grow & Reproduce
- The Human Respiratory System
- The Human Cardiovascular System
- The Human Digestive System
- The Human Endocrine Systems
- The Human Nervous System
- The Human Muscular System
- The Human Skeletal System
IN THE NEWS

Our mission is to provide high quality online tutoring services, using state of the art Internet technology, to school students worldwide.
Online test prep and practice
SCAT
SSAT
ISEE
PSAT
SAT
ACT
AP Exam
Science Tutoring
Physics Tutoring
Chemistry Tutoring
Biology Tutoring
Math Tutoring
Pre-Algebra Tutoring
Algebra Tutoring
Pre Calculus Tutoring
Calculus Tutoring
Geometry Tutoring
Trigonometry Tutoring
Statistics Tutoring
Quick links
Free Worksheets
Fact sheet
Sales Partner Opportunities
Parents
Passive Fundraising
Virtual Fundraising
Our Expert Tutors
Safe and Secure Tutoring
Interactive Online Tutoring
After School Tutoring
Elementary School Tutoring
Middle School Tutoring
High School Tutoring
Home Work Help
Math Tutors New York City
Press
©2022 eTutorWorld Terms of use Privacy Policy Site by Little Red Bird
©2022 eTutorWorld
Terms of use
Privacy Policy
Site by Little Red Bird









