Fractional Exponents
Grade 6 Math Worksheets
Fractional exponents are a way to represent a number that is being raised to a fractional power. In other words, it’s when we use a fraction instead of a whole number as the exponent. The number being raised to a power is called the base.
In this article, we will cover:
- 5 Fractional Exponent Rules
- How to Simplify Fractional Factors?
- How to Multiply Fractional Exponents with the Same Bases?
- How to Multiply Fractional Exponents with the Different Bases?
- Dividing Fractional Exponents
- Negative Fractional Exponents
- FAQs
Fractional Exponents - Grade 6 Math Worksheet PDF
This is a free printable / downloadable PDF worksheet with practice problems and answers. You can also work on it online.
|
Untimed | |
Sign up with your email ID to access this free worksheet.
"We really love eTutorWorld!"
"We really love etutorworld!. Anand S and Pooja are excellent math teachers and are quick to respond with requests to tutor on any math topic!" - Kieran Y (via TrustSpot.io)
"My daughter gets distracted easily"
"My daughter gets distracted very easily and Ms. Medini and other teachers were patient with her and redirected her back to the courses.
With the help of Etutorworld, my daughter has been now selected in the Gifted and Talented Program for the school district"
- Nivea Sharma (via TrustSpot.io)
In the number, say x1/y, x is the base and 1/y is the fractional exponent.
For example, in the expression 2^(3/2), 2 is the base and (3/4) is the fractional exponent. This means that 2 is being multiplied by itself 3/4 times. When we raise a number to a fractional exponent, we are taking the root of the number. So, 2^(3/2) is the same as the square root of 2 raised to the power of 3.
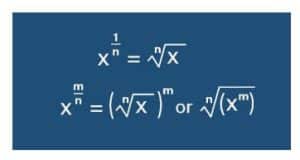
Fractional Exponent Rules
The rules for working with fractional exponents are similar to those for working with integer exponents, but with a few important differences.
1. Product of Fractional Exponents
When you multiply two numbers with fractional exponents, you can add the exponents.
For example, a1/m × a1/n = a(1/m + 1/n)
For example, (2^(3/4)) * (2^(1/2)) = 2^((3/4) + (1/2)) = 2^(5/4)
2. Quotient of Fractional Exponents
When you divide two numbers with fractional exponents, you can subtract the exponents.
For example, a1/m ÷ a1/n = a(1/m – 1/n)
For example, (2^(3/4)) / (2^(1/2)) = 2^((3/4) – (1/2)) = 2^(1/4)
3. Power of a Power
When you raise a number with a fractional exponent to another power, you can multiply the exponents.
For example, (a^m)^n = a^(mn) where m and n are fractional exponents.
For example, (2^(3/4))^2 = 2^((3/4) * 2) = 2^(3/2)
4. Power of a Product
When you raise a product of numbers to a fractional exponent, you can distribute the exponent to each term.
For example, (ab)^n = (a^n)(b^n)
For example, (3*4)^(1/2) = (3^(1/2))(4^(1/2)) = (sqrt(3))*(2)
5. Power of a Quotient
When you raise a quotient of numbers to a fractional exponent, you can distribute the exponent to each term and change the sign of the exponent of the denominator.
For example, a1/m ÷ b1/m = (a÷b)1/m
For example, (3/4)^(2/3) = (3^(2/3))/(4^(2/3)) = (3^(2/3))/(4^(2/3))

It’s important to note that when working with fractional exponents, it’s necessary to be familiar with the properties of radicals and the basic operations with fractions. Also, these rules apply when the base of the fractional exponent is the same.
Simplifying Fractional Factors
Simplifying fractional exponents is the process of rewriting an expression with a fractional exponent in a simpler form. This can be done by using the properties of exponents and the rules for working with fractional exponents.
1. Using the reciprocal property
When the exponent of a number is a fraction, we can simplify it by using the reciprocal property.
For example, (a^m)^(1/n) = a^(m/n), where m and n are integers and n is not equal to zero.
For example, (2^(3/4)) = (2^(3/4))^(4/4) = 2^(3/4 * 4/4) = 2^(3/1) = 8
2. Using the properties of radicals
When the exponent of a number is a fraction, it can also be simplified by using the properties of radicals.
For example, a^(m/n) = (sqrt(a^m))^n, where m and n are integers and n is not equal to zero.
For example, (2^(3/4)) = (sqrt(2^3))^(4/4) = (sqrt(8))^(4/4) = 2^(2/1) = 4
3. Combining like terms
When an expression contains several terms with the same base and exponent, we can simplify it by combining like terms.
For example, (2^(3/4))(2^(3/4))(2^(3/4)) = (2^(3/4))^3 = 2^(3/4 * 3) = 2^(9/4)
4. Combining the above methods
we can simplify fractional exponents by combining the above methods.
For example, (2^(3/4))(2^(1/2)) = (2^(3/4))(sqrt(2^1)) = 2^(3/4 + 1/2) = 2^(5/4)
It’s important to note that when simplifying fractional exponents, it’s important to be familiar with the properties of radicals and the basic operations with fractions. Also, to simplify the expressions, it’s important to use the appropriate property or rule depending on the form of the expression.

Multiplying Fractional Exponents with Same Bases
When multiplying fractional exponents with the same base, we can add the exponents. This is because when we multiply two numbers with the same base and different exponents, we are multiplying them together multiple times.
For example, if we have the expression (a^m) * (a^n), where a is the base and m and n are the exponents, we can simplify it by adding the exponents: (a^m) * (a^n) = a^(m+n) or if we have fractional exponents then we can solve the problem as a1/m × a1/n = a(1/m + 1/n) where 1/m and 1/n are fractional exponents.
For example, (2^(3/4)) * (2^(1/2)) = 2^(3/4 + 1/2) = 2^(5/4)
It’s important to note that this rule only applies when the bases of the fractional exponents are the same. If the bases are different, we cannot add the exponents and we have to simplify the expression using other methods.
It’s also important to keep in mind that when adding the exponents, the fraction should have the same denominator, if not we have to find the common denominator before adding the exponents.
In summary, when multiplying fractional exponents with the same base, we can add the exponents to simplify the expression. This is because we are multiplying the base multiple times and this can be represented by adding the exponents.
Multiplying Fractional Exponents with Different Bases
When multiplying fractional exponents with different bases, we cannot add the exponents. This is because the bases are different and therefore the exponents cannot be combined in the same way as when the bases are the same. Instead, we have to leave the exponents in their original form and multiply the bases as normal, For example, if we have the expression (a^m) * (b^n), where a and b are the bases and m and n are the exponents, we can simplify it by multiplying the bases and keeping the exponents as they are: (a^m) * (b^n) = (ab)^(mn)
For example, (2^(3/4)) * (3^(1/2)) = (2*3)^(3/4 * 1/2) = (6)^(3/8)
It’s important to note that in this case, we can’t simplify the expression any further, and the result is the product of the bases raised to the power of the product of the exponents.
It’s also important to keep in mind that when multiplying the bases, we should be familiar with the basic operations with fractions and the properties of radicals, so we can simplify the product of the bases if needed.
In summary, when multiplying fractional exponents with different bases, we have to multiply the bases and keep the exponents as they are. This is because the bases are different and cannot be combined in the same way as when the bases are the same. The result is the product of the bases raised to the power of the product of the exponents, which can’t be simplified further.
“There have been times when we booked them last minute, but the teachers have been extremely well-prepared and the help desk at etutorworld is very prompt.
Our kid is doing much better with a higher score.”
6th Grade Tutoring
eTutorWorld offers Personalized Online Tutoring for Math, Science, English, and Standardised Tests.
Our Tutoring Packs start at just under $22.49 per hour, and come with a moneyback guarantee.
Schedule a FREE Trial Session, and experience quality tutoring for yourself. (No credit card required.)
Dividing Fractional Exponents
Dividing fractional exponents with the same base is similar to multiplying them, but instead of adding the exponents, we subtract them. This is because when we divide two numbers with the same base and different exponents, we are dividing one by the other.
For example, if we have the expression (a^m) / (a^n), where a is the base and m and n are the exponents, we can simplify it by subtracting the exponents: (a^m) / (a^n) = a^(m-n) or a1/m ÷ a1/n = a(1/m – 1/n) where 1/m and 1/n are fractional exponents.
For example, (2^(3/4)) / (2^(1/2)) = 2^(3/4 – 1/2) = 2^(1/4)
It’s important to note that this rule only applies when the bases of the fractional exponents are the same. If the bases are different, we cannot subtract the exponents and we have to simplify the expression using other methods.
It’s also important to keep in mind that when subtracting the exponents, the fraction should have the same denominator, if not we have to find the common denominator before subtracting the exponents.
In summary, when dividing fractional exponents with the same base, we can subtract the exponents to simplify the expression. This is because we are dividing one by the other and this can be represented by subtracting the exponents.
Negative Fractional Exponents
Negative fractional exponents are exponents that have a negative value in the form of a fraction. They are also known as reciprocal exponents. They are used to represent the reciprocal of a number raised to a power.
For example, when we have a number “a” raised to a power of “-m/n” where m and n are integers and n is not equal to zero, it can be rewritten as: a^(-m/n) = 1/(a^(m/n))
For example, 2^(-3/4) = 1/(2^(3/4)) = 1/8
It’s important to note that when we have a negative exponent, we are taking the reciprocal of the number raised to a power, that means dividing 1 by the number raised to a power.
Also, when we have a negative fractional exponent, we can simplify the expression by using the reciprocal property, that means the reciprocal of a number raised to a power is the same as one divided by the number raised to the power.
In summary, negative fractional exponents are exponents that have a negative value in the form of a fraction. They are used to represent the reciprocal of a number raised to a power, meaning dividing 1 by the number raised to the power. We can simplify negative fractional exponents by using the reciprocal property, that means the reciprocal of a number raised to a power is the same as one divided by the number raised to the power.
Do You Stack Up Against the Best?
If you have 30 minutes, try our free diagnostics test and assess your skills.
Fractional Exponents FAQS
What are fractional exponents?
Fractional exponents are a way to represent a number that is being raised to a fractional power. In other words, it’s when we use a fraction instead of a whole number as the exponent. The number being raised to the power is called the base.
How do I simplify an expression with a fractional exponent?
You can simplify an expression with a fractional exponent by using the properties of exponents and the rules for working with fractional exponents. This includes using the reciprocal property, properties of radicals, combining like terms and combining the above methods.
How do I multiply fractional exponents with the same base?
When multiplying fractional exponents with the same base, you can add the exponents. This is because we are multiplying the base multiple times and this can be represented by adding the exponents.
How do I divide fractional exponents with the same base?
When dividing fractional exponents with the same base, you can subtract the exponents. This is because we are dividing one by the other and this can be represented by subtracting the exponents.
How do I deal with negative fractional exponents?
When dealing with negative fractional exponents, it means that you need to find the reciprocal of the number raised to a power. This can be done by using the reciprocal property, that means the reciprocal of a number raised to a power is the same as one divided by the number raised to the power.
Are fractional exponents only used in Algebra?
Fractional exponents are a useful tool in mathematics, especially in Algebra, however, they are also used in other branches of mathematics, such as Calculus, Statistics, and others.
Can you simplify all expressions with fractional exponents?
Not all expressions with fractional exponents can be simplified. However, using the properties of exponents and the rules for working with fractional exponents we can greatly simplify the expression.

Gloria Mathew writes on math topics for K-12. A trained writer and communicator, she makes math accessible and understandable to students at all levels. Her ability to explain complex math concepts with easy to understand examples helps students master math. LinkedIn
Affordable Tutoring Now Starts at Just $22.49
eTutorWorld offers affordable one-on-one live tutoring over the web for Grades K-12. We are also a leading provider of Test Prep help for Standardized Tests (SCAT, CogAT, MAP, SSAT, SAT, ACT, ISEE, and AP).
What makes eTutorWorld stand apart are: flexibility in lesson scheduling, quality of hand-picked tutors, assignment of tutors based on academic counseling and diagnostic tests of each student, and our 100% money-back guarantee.
Whether you have never tried personalized online tutoring before or are looking for better tutors and flexibility at an affordable price point, schedule a FREE TRIAL Session with us today.
*There is no purchase obligation or credit card requirement
Grade 6 Science Worksheets
- Inquiry process
- Nature of Science
- Scientific Inquiry
- Inquiry, Analysis and Problem Solving
- Ethical Practices
- Science and Society
- Biotic and Abiotic Factors
- Impact of Organisms
- Adaptation
- Spheres of Earth
- Natural Resources
- Environmental Issues
- Conservation of Earth
- Understanding Technology
- Abilities To Do Technological Design
- Structure of Earth
- Solar System
- Rocks and Fossils
- Earth Systems
- Plate Tectonics
- Evolution
- Magnetic Field of Earth
- Geologic Time
- Materials and Processes That Shape a Planet
- Astronomy
- Ecology
- Energy
- Kinetic and Potential Energy
- Energy Transfer
- Matter and its Structure
- States of Matter
- Physical and Chemical Changes
- Force and Motion
- Electricity and Magnetism
- Wave Interactions
- Sound
- Light
- Introduction to Life Science
- The Origin & History of Life On Earth
- Plant and Animal Cells
- Parts of a Cell
- The Cell Cycle
- How Living Organisms Get Energy
- Classification of Organisms
- How Plants Grow & Reproduce
- The Human Respiratory System
- The Human Cardiovascular System
- The Human Digestive System
- The Human Endocrine Systems
- The Human Nervous System
- The Human Muscular System
- The Human Skeletal System
IN THE NEWS

Our mission is to provide high quality online tutoring services, using state of the art Internet technology, to school students worldwide.
Online test prep and practice
SCAT
SSAT
ISEE
PSAT
SAT
ACT
AP Exam
Science Tutoring
Physics Tutoring
Chemistry Tutoring
Biology Tutoring
Math Tutoring
Pre-Algebra Tutoring
Algebra Tutoring
Pre Calculus Tutoring
Calculus Tutoring
Geometry Tutoring
Trigonometry Tutoring
Statistics Tutoring
Quick links
Free Worksheets
Fact sheet
Sales Partner Opportunities
Parents
Passive Fundraising
Virtual Fundraising
Our Expert Tutors
Safe and Secure Tutoring
Interactive Online Tutoring
After School Tutoring
Elementary School Tutoring
Middle School Tutoring
High School Tutoring
Home Work Help
Math Tutors New York City
Press
©2022 eTutorWorld Terms of use Privacy Policy Site by Little Red Bird
©2022 eTutorWorld
Terms of use
Privacy Policy
Site by Little Red Bird










