Area of a Parallelogram
Grade 6 Math Worksheets
A parallelogram is a 2-dimensional geometric shape that has opposite sides that are parallel and equal in length. It is a quadrilateral that has two pairs of parallel sides.
In this article, you will learn
- Steps for finding the area of a parallelogram
- Tips for accurately measuring the base and height of a parallelogram
- Applications of finding the area of a parallelogram
- Summary of the steps involved in finding the area of a parallelogram
- FAQs
Area of a Parallelogram - Grade 6 Math Worksheet PDF
This is a free printable / downloadable PDF worksheet with practice problems and answers. You can also work on it online.
|
Untimed | |
Sign up with your email ID to access this free worksheet.
"We really love eTutorWorld!"
"We really love etutorworld!. Anand S and Pooja are excellent math teachers and are quick to respond with requests to tutor on any math topic!" - Kieran Y (via TrustSpot.io)
"My daughter gets distracted easily"
"My daughter gets distracted very easily and Ms. Medini and other teachers were patient with her and redirected her back to the courses.
With the help of Etutorworld, my daughter has been now selected in the Gifted and Talented Program for the school district"
- Nivea Sharma (via TrustSpot.io)
The purpose of this article is to provide an overview of how to find the area of a parallelogram and understand the formula used to calculate the area.
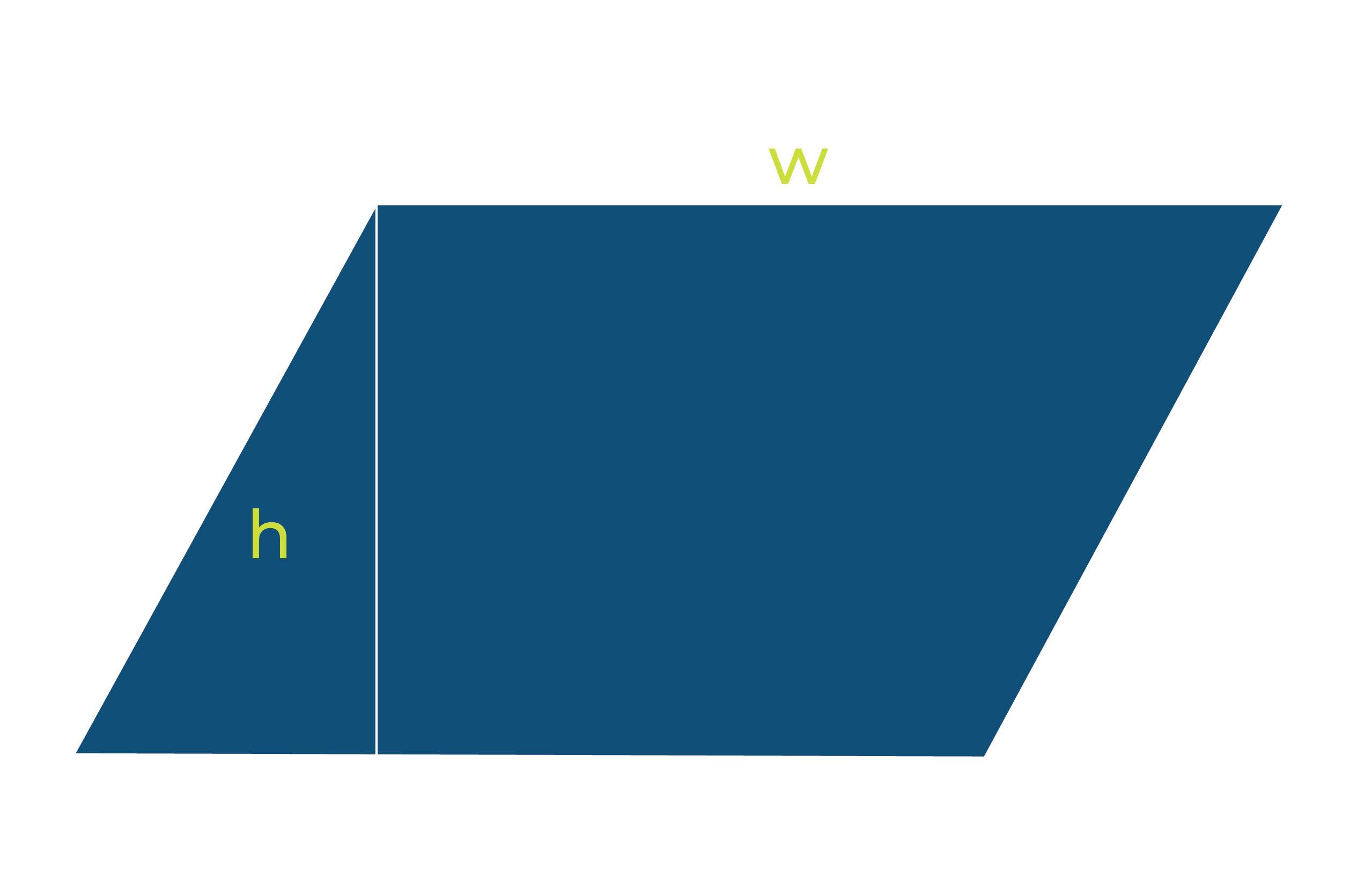
Steps for finding the area of a parallelogram
Measuring the base and height of the parallelogram: The first step in finding the area of a parallelogram is to measure the length of the base (b) and height (h) of the parallelogram. This can be done using a ruler or measuring tape.
Using the formula A = b * h to calculate the area: Once the base and height have been measured, the next step is to use the formula A = b * h to calculate the area of the parallelogram. The formula is straightforward: multiply the length of the base by the height.
The formula A = b * h is used to calculate the area of a parallelogram. The base (b) is multiplied by the height (h) to give the total area of the parallelogram.
The base and height of the parallelogram are crucial in determining the area of the parallelogram. A change in either the base or height will result in a different calculated area, so it is important to measure both accurately.
Let’s solve this example, what is the area of a parallelogram with a base equal to 4 cm and a height equal to 7 cm?
The base length of the parallelogram = 4 cm
Height of the parallelogram = 7 cm
Area of the parallelogram = base x height = 4cm x 7cm = 28 cm^2
Tips for accurately measuring the base and height of a parallelogram
In order to accurately find the area of a parallelogram, it is important to use precise measuring tools. A ruler or measuring tape should be used to measure the length of the base and height. A measurement that is even slightly off can result in a significant difference in the calculated area.
To ensure that the measurements are accurate, it is important to measure the length of the base and height carefully. A few tips include making sure the measuring tool is placed precisely on the edge of the parallelogram, measuring in a straight line, and measuring both the base and height twice to check for consistency.
“There have been times when we booked them last minute, but the teachers have been extremely well-prepared and the help desk at etutorworld is very prompt.
Our kid is doing much better with a higher score.”
6th Grade Tutoring
eTutorWorld offers Personalized Online Tutoring for Math, Science, English, and Standardised Tests.
Our Tutoring Packs start at just under $22.49 per hour, and come with a moneyback guarantee.
Schedule a FREE Trial Session, and experience quality tutoring for yourself. (No credit card required.)
Applications of finding the area of a parallelogram
Real-world examples of using the area of a parallelogram: The area of a parallelogram is used in many real-world applications, such as determining the square footage of a room, calculating the area of a rectangular pool, and determining the size of a field for sports or farming purposes.
Importance of understanding how to find the area of a parallelogram: Understanding how to find the area of a parallelogram is important for many real-world applications and for solving mathematical problems. The ability to calculate the area of a parallelogram accurately and efficiently is a valuable skill for anyone working in various fields, from construction and engineering to mathematics and science.
Summary of the steps involved in finding the area of a parallelogram:
To find the area of a parallelogram, the first step is to measure the length of the base (b) and height (h) of the parallelogram. Next, use the formula A = b * h to calculate the area by multiplying the base by the height.
Let us understand it with an example, The perimeter of a parallelogram is 30 cm. If the height of the parallelogram is 5 cm and the length of the adjacent side is 6 cm, find its area.
The solution would be as follow:
Perimeter of parallelogram = 30 cm
Height = 5cm
Length of adjacent sides = 6 cm
Perimeter of parallelogram = 2 (Adjacent side + Base) = 2 (6 + B)
30 = 2 (6 + B)
6 + B = 15
B = 15 – 6 = 9 cm
Now,
Area of parallelogram = Base x height
= 9 x 5
= 45 cm^2
Finding the area of a parallelogram is a fundamental skill that is useful in a variety of real-world applications, as well as for solving mathematical problems. Understanding how to accurately measure the base and height, and using the formula A = b * h to calculate the area, is an important aspect of this skill. By following these steps, anyone can successfully find the area of a parallelogram
Do You Stack Up Against the Best?
If you have 30 minutes, try our free diagnostics test and assess your skills.
Area of a Parallelogram FAQS
What is the formula for finding the area of a parallelogram?
The formula for finding the area of a parallelogram is A = b * h, where b is the length of the base and h is the height of the parallelogram.
Is the formula for finding the area of a parallelogram different than the formula for finding the area of a rectangle?
No, the formula for finding the area of a parallelogram is the same as the formula for finding the area of a rectangle.
How important is accurately measuring the base and height of a parallelogram?
Accurately measuring the base and height is crucial in determining the area of a parallelogram. A small measurement error can result in a significantly different calculated area.
What tools should be used to measure the base and height of a parallelogram?
A ruler or measuring tape should be used to measure the length of the base and height of a parallelogram.
Can the formula for finding the area of a parallelogram be used for any other geometric shapes?
No, the formula for finding the area of a parallelogram can only be used for parallelograms. Different formulas are used for finding the area of other geometric shapes, such as triangles and circles.
What are some real-world applications of finding the area of a parallelogram?
Finding the area of a parallelogram is used in many real-world applications, such as determining the square footage of a room, calculating the area of a rectangular pool, and determining the size of a field for sports or farming purposes.

Gloria Mathew writes on math topics for K-12. A trained writer and communicator, she makes math accessible and understandable to students at all levels. Her ability to explain complex math concepts with easy to understand examples helps students master math. LinkedIn
Affordable Tutoring Now Starts at Just $22.49
eTutorWorld offers affordable one-on-one live tutoring over the web for Grades K-12. We are also a leading provider of Test Prep help for Standardized Tests (SCAT, CogAT, MAP, SSAT, SAT, ACT, ISEE, and AP).
What makes eTutorWorld stand apart are: flexibility in lesson scheduling, quality of hand-picked tutors, assignment of tutors based on academic counseling and diagnostic tests of each student, and our 100% money-back guarantee.
Whether you have never tried personalized online tutoring before or are looking for better tutors and flexibility at an affordable price point, schedule a FREE TRIAL Session with us today.
*There is no purchase obligation or credit card requirement
Grade 6 Science Worksheets
- Inquiry process
- Nature of Science
- Scientific Inquiry
- Inquiry, Analysis and Problem Solving
- Ethical Practices
- Science and Society
- Biotic and Abiotic Factors
- Impact of Organisms
- Adaptation
- Spheres of Earth
- Natural Resources
- Environmental Issues
- Conservation of Earth
- Understanding Technology
- Abilities To Do Technological Design
- Structure of Earth
- Solar System
- Rocks and Fossils
- Earth Systems
- Plate Tectonics
- Evolution
- Magnetic Field of Earth
- Geologic Time
- Materials and Processes That Shape a Planet
- Astronomy
- Ecology
- Energy
- Kinetic and Potential Energy
- Energy Transfer
- Matter and its Structure
- States of Matter
- Physical and Chemical Changes
- Force and Motion
- Electricity and Magnetism
- Wave Interactions
- Sound
- Light
- Introduction to Life Science
- The Origin & History of Life On Earth
- Plant and Animal Cells
- Parts of a Cell
- The Cell Cycle
- How Living Organisms Get Energy
- Classification of Organisms
- How Plants Grow & Reproduce
- The Human Respiratory System
- The Human Cardiovascular System
- The Human Digestive System
- The Human Endocrine Systems
- The Human Nervous System
- The Human Muscular System
- The Human Skeletal System
IN THE NEWS

Our mission is to provide high quality online tutoring services, using state of the art Internet technology, to school students worldwide.
Online test prep and practice
SCAT
SSAT
ISEE
PSAT
SAT
ACT
AP Exam
Science Tutoring
Physics Tutoring
Chemistry Tutoring
Biology Tutoring
Math Tutoring
Pre-Algebra Tutoring
Algebra Tutoring
Pre Calculus Tutoring
Calculus Tutoring
Geometry Tutoring
Trigonometry Tutoring
Statistics Tutoring
Quick links
Free Worksheets
Fact sheet
Sales Partner Opportunities
Parents
Passive Fundraising
Virtual Fundraising
Our Expert Tutors
Safe and Secure Tutoring
Interactive Online Tutoring
After School Tutoring
Elementary School Tutoring
Middle School Tutoring
High School Tutoring
Home Work Help
Math Tutors New York City
Press
©2022 eTutorWorld Terms of use Privacy Policy Site by Little Red Bird
©2022 eTutorWorld
Terms of use
Privacy Policy
Site by Little Red Bird










