Creating Isosceles Triangles

An isosceles triangle is a special type of triangle with two sides of equal length. This characteristic creates a unique balance in the triangle’s shape, giving it an appearance of symmetry. The angles opposite the equal sides are also equal, contributing to its intriguing geometry.

As you explore the world of triangles, watch for these fascinating isosceles triangles that exhibit such captivating patterns.

Unlocking Geometric Artistry: Constructing Isosceles Triangles

Welcome to a journey of geometric discovery! In geometry, triangles are the building blocks of countless shapes and structures. Among these, the isosceles triangle stands out with its symmetrical allure and intriguing properties.

In this guide, we’ll systematically explore the art of constructing isosceles triangles. With a compass and a straightedge in hand, you’re about to embark on a creative endeavor to deepen your understanding of angles, lines, and symmetry. As you follow these instructions, you’ll uncover the secrets behind crafting these captivating triangles, each step enhancing your grasp of geometry.

So, let’s delve into the world of isosceles triangles – where equal sides converge, angles harmonize, and geometry becomes an art form. Get ready to create and explore the beauty of these unique triangles!

Type 1 – Constructing Isosceles Triangles with Given Side Lengths

Today’s adventure takes us into isosceles triangles, where we’ll construct these captivating shapes step by step. Unlike some explorations, where we start with a blank canvas, this time we’re given the lengths of all sides, and our task is to breathe life into this triangle.

Let’s embark on this journey of construction:

Given:

• Side AB = Side AC (Both sides are equal)
• Side BC (A different length)

Materials Needed:

• Compass
• Straightedge (ruler)

Steps:

1. Base Line: Draw a straight line segment using your straightedge and label the endpoints as A and B. It will be the base of our triangle.
2. Side BC: On the line segment AB, measure the length of side BC from point B. Mark this point as C.
3. Compass Center: Set your compass point at point A and open it to a length equal to the given side BC. Make an arc intersecting the line segment AB above point A. Mark this intersection as point D.
4. Arcs for Equal Sides: With point D as the center, open your compass to the length of side BC again. Draw arcs on both sides of line segment AB. These arcs will intersect the line above points B and C.
5. Connect Points: Use your straightedge to draw line segments AD and CD, connecting points A and D, and D and C, respectively. It completes your isosceles triangle ABC.

Type 2 – Constructing Triangles with Given Sides and Angle

Given:

• Side AB = Side AC (Both sides are equal)
• Angle BAC (Angle between the equal sides)

Materials Needed:

• Compass
• Protractor (for measuring angles)
• Straightedge (ruler)

Steps:

1. Base Line: Start by drawing a straight line segment using your straightedge. Label the endpoints as A and B. It will serve as the base of your triangle.
2. Angle BAC: Use your protractor to measure and mark the given angle BAC at point A. It will establish the direction of the equal sides.
3. Equal Sides: Place your compass point at point A and adjust its width to the length of the given equal sides (AB or AC). Draw arcs on both sides of the angle, intersecting the lines you previously drew.
4. Triangle Vertex: Where the arcs intersect the line, label the points of intersection as C and D.
5. Connect the Points: Use your straightedge to draw line segments AC and AD, connecting points A to C and A to D. This completes your isosceles triangle ABC.

Type 3 – Crafting Triangles with a Given Base and Adjacent Angles

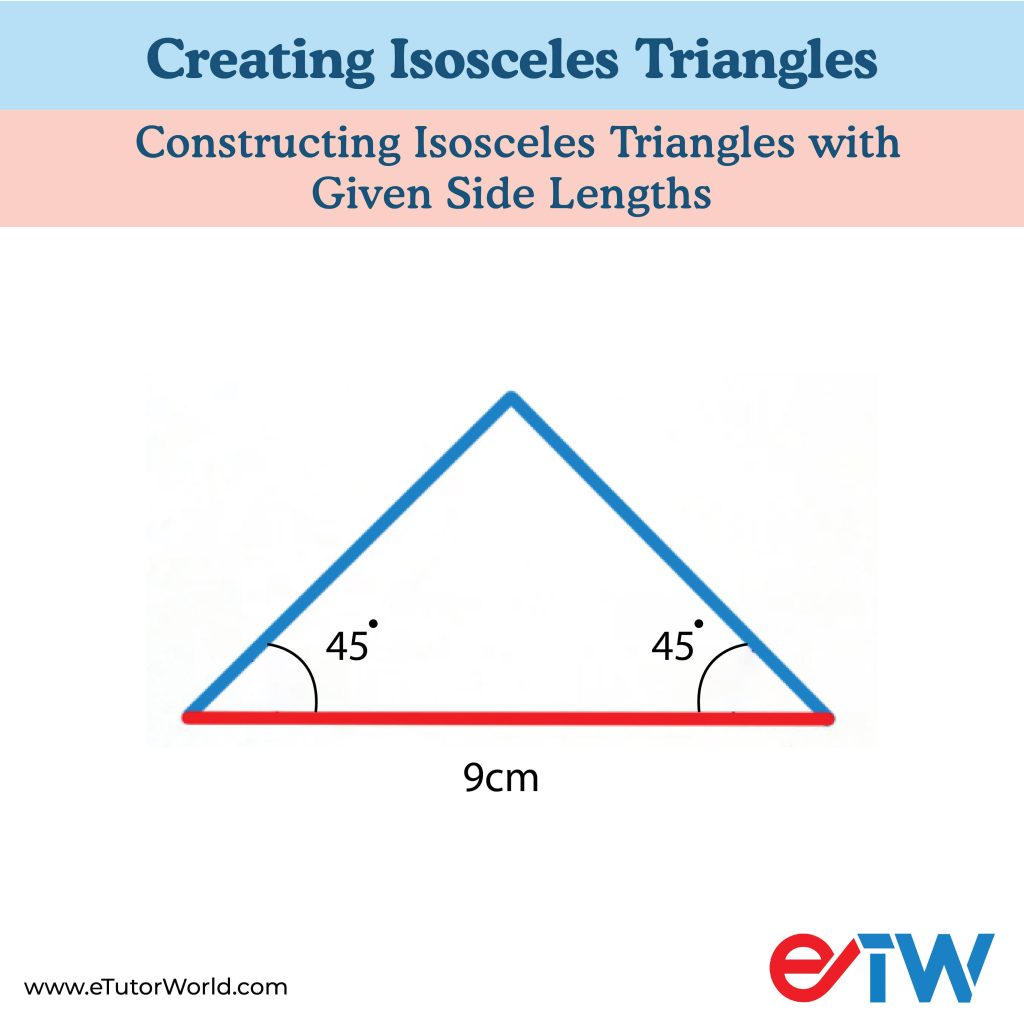
Given:

• Base AB (Length of the base)
• Adjacent angles ∠BAC and ∠CAB (Angles adjacent to the base)

Materials Needed:

• Compass
• Protractor (for measuring angles)
• Straightedge (ruler)

Steps:

1. Base Line: Begin by drawing a straight line segment using your straightedge. Label the endpoints as A and B. This line will serve as the base of our triangle.
2. Adjacent Angles: Use your protractor to measure and mark the given adjacent angles ∠BAC and ∠CAB, at points A and B, respectively. These angles provide the direction for the equal sides.
3. Equal Sides Arcs: Place your compass point at point A and set its width to the desired length of the equal sides (AB or AC). Draw arcs on both sides of angle ∠BAC, intersecting the line segment.
4. Triangle Vertex: Label the points where the arcs intersect the line as C and D.
5. Connect the Points: Use your straightedge to draw line segments BC and BD, connecting points B to C and B to D. This completes your isosceles triangle ABC.

Type 4 – Crafting Triangles with a Given Base and Altitude

Given:

• Base AB (Length of the base)
• Altitude CD (Length of the altitude from the base)

Materials Needed:

• Compass
• Straightedge (ruler)

Steps:

1. Base Line: Start by drawing a straight line segment using your straightedge. Label the endpoints as A and B. This line represents the base of the triangle.
2. Altitude CD: Use your straightedge to draw a perpendicular line segment from point C to the base AB. Label the point of intersection as D. This is the altitude of the triangle.
3. Equal Sides Arcs: Place your compass point at point D and adjust its width to the given altitude CD. Draw arcs on both sides of the base AB, intersecting the lines you previously drew.
4. Triangle Vertex: Where the arcs intersect the base, label the points of intersection as E and F.
5. Connect the Points: Use your straightedge to draw line segments CE and DF, connecting points C to E and D to F. This completes your isosceles triangle ABC.

Now equipped with the skills to create isosceles triangles, you’re ready to uncover the elegance of geometric constructions. Every construction is an opportunity to discover both mathematical principles and your creative problem-solving prowess. Enjoy your explorations!

FAQs

Grade 7 Science Worksheets

• Elements and Compounds
• Solar Energy
• Photosynthesis
• Electricity and Magnetism
• Law of conservation of energy
• Periodic table
• Properties of Matter
• Waves
• Energy Resources 
• Weather and Climate
• Immune, Circulatory and Digestive Systems
• Organs in Multi-cellular Organism
• Sedimentary, Igneous, and Metamorphic Rocks
• Structure of the Earth
• Law of Conservation of Mass
• Physical and Chemical Changes
• Scientific Method
• Human Digestive System
• Environmental Science
• Renewable and Non-renewable energy Resources
• Characteristics of Living Organisms
• Life Science
• Earth and Space Science
• Solar Eclipse
• Heat Technology
• Newton’s Laws of Motions
• Physical Science
• Tools, Measurement and SI Units
• Earth Atmosphere
• Interactions of Living things
• The Earth Ecosystem
• Organelles in Plant and Animal cells
• Layers of the Earth
• Cycles in Nature

Grade 7 Math Worksheets

• Fractions
• Linear equations word problems
• Statistics
• Properties of Parallel Line
• Finding slope from an equation
• Identifying Quadrilaterals
• Percent Change
• Properties of addition and multiplication
• Pythagorean Theorem
• Solving two step inequalities
• Symmetry
• Fractions to Decimals (New)
• Whole Number Exponents with Integer Bases (New)
• Adding and Subtracting Fractions (New)
• Integer Addition and Subtraction (New)
• Dividing Mixed Numbers (New)
• Basics of Coordinate Geometry (New)