Solid Geometry

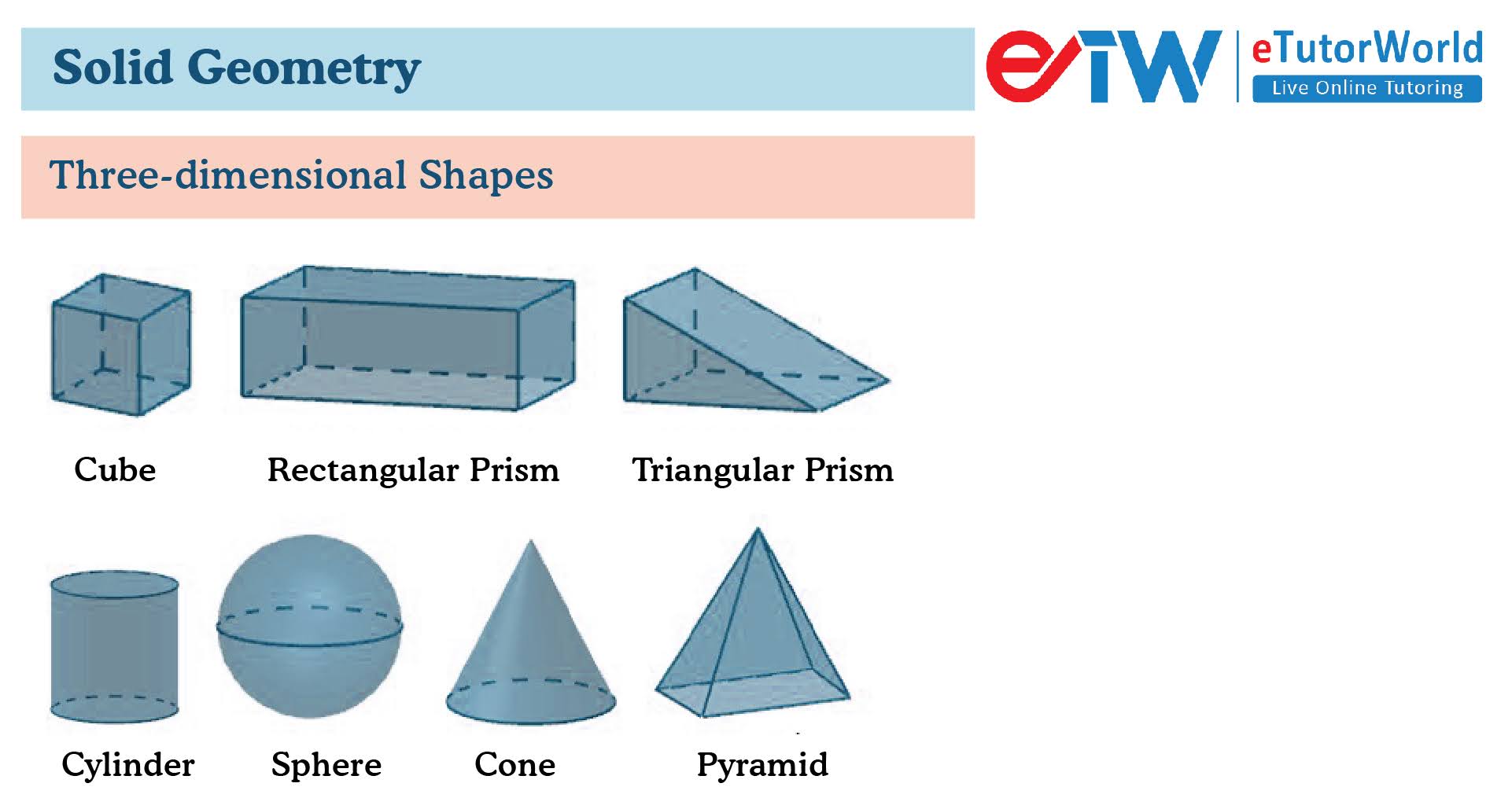
Solid geometry is a branch of geometry that deals with the study of three-dimensional shapes, also known as solids. It involves the study of properties such as volume, surface area, angles, and edges of various three-dimensional shapes, such as prisms, pyramids, spheres, cylinders, cones, and tori.

Table of Contents:

• Solid geometry
• Volume
• Solved Examples for Volume
• Surface Area
• Solved Examples for Surface Area
• Polyhedra
• Solved Examples for Polyhedra

Solid Geometry

Solid geometry is an important area of study in mathematics and has many applications in fields such as engineering, architecture, and physics. It is used in designing and building structures such as buildings, bridges, and tunnels, and in creating models of physical objects and systems.

Some key concepts in solid geometry include:

Volume: The amount of space occupied by a three-dimensional object is known as its volume. The volume of a solid is typically measured in cubic units.

Surface area: The total area of all the surfaces of a three-dimensional object is known as its surface area. The surface area of a solid is typically measured in square units.

Polyhedra: A polyhedron is a three-dimensional object with flat faces, straight edges, and sharp corners. Examples include cubes, prisms, pyramids, and tetrahedra.

Spheres: A sphere is a three-dimensional object with a curved surface where all points on the surface are equidistant from the center point. Spheres are used to model objects such as planets, marbles, and balls.

Cylinders: A cylinder is a three-dimensional object with two parallel, circular bases and a curved surface connecting the bases. Cylinders are used to model objects such as cans, tubes, and pipes.

Cones: A cone is a three-dimensional object with a circular base and a curved surface that tapers to a point. Cones are used to model objects such as ice cream cones, party hats, and traffic cones.

Solid geometry involves the use of formulas and mathematical equations to calculate the various properties of three-dimensional objects, such as the volume and surface area of a sphere or the surface area and lateral area of a cylinder.

Volume

Volume is a measurement of the amount of space that a three-dimensional object occupies. In solid geometry, volume is typically measured in cubic units, such as cubic meters, cubic centimeters, or cubic feet.

The formula for calculating the volume of a solid depends on the shape of the object. Here are some formulas for calculating the volume of common solid shapes:

Rectangular prism: The volume of a rectangular prism is given by the formula V = l x w x h, where l, w, and h are the lengths of the three dimensions of the rectangular prism.

Cube: The volume of a cube is given by the formula V = s^3, where s is the length of one of the sides of the cube.

Cylinder: The volume of a cylinder is given by the formula V = πr^2h, where r is the radius of the circular base and h is the height of the cylinder.

Sphere: The volume of a sphere is given by the formula V = (4/3)πr^3, where r is the radius of the sphere.

Cone: The volume of a cone is given by the formula V = (1/3)πr^2h, where r is the radius of the circular base and h is the height of the cone.

Calculating the volume of a solid can be useful in various real-world situations, such as determining the amount of space needed to store a certain quantity of material or calculating the amount of material needed to fill a particular space.

Solved Examples for Volume

Sure, here are some examples of calculating the volume of common three-dimensional shapes:

Find the volume of a rectangular prism with a length of 5 meters, a width of 3 meters, and a height of 2 meters.
Solution: Using the formula V = l x w x h, we have V = 5 x 3 x 2 = 30 cubic meters. Therefore, the volume of the rectangular prism is 30 cubic meters.

Find the volume of a cube with a side length of 6 centimeters.
Solution: Using the formula V = s^3, we have V = 6^3 = 216 cubic centimeters. Therefore, the volume of the cube is 216 cubic centimeters.

Find the volume of a cylinder with a radius of 4 meters and a height of 8 meters.
Solution: Using the formula V = πr^2h, we have V = π x 4^2 x 8 = 128π cubic meters (approx. 402.12 cubic meters). Therefore, the volume of the cylinder is 128π cubic meters.

Find the volume of a sphere with a radius of 3 inches.
Solution: Using the formula V = (4/3)πr^3, we have V = (4/3)π x 3^3 = 36π cubic inches (approx. 113.1 cubic inches). Therefore, the volume of the sphere is 36π cubic inches.

Find the volume of a cone with a radius of 5 centimeters and a height of 10 centimeters.
Solution: Using the formula V = (1/3)πr^2h, we have V = (1/3)π x 5^2 x 10 = 83.33 cubic centimeters (approx. 261.78 cubic centimeters). Therefore, the volume of the cone is 83.33 cubic centimeters.

Surface area

Surface area is a measure of the total area that the surface of a three-dimensional object occupies. It is expressed in square units such as square meters, square centimeters, or square feet. The formula for calculating the surface area of an object depends on the shape of the object.

Here are some formulas for calculating the surface area of common three-dimensional objects:

Rectangular Prism: The surface area of a rectangular prism is given by the formula A = 2lw + 2lh + 2wh, where l, w, and h are the lengths of the three dimensions of the rectangular prism.

Cube: The surface area of a cube is given by the formula A = 6s^2, where s is the length of one of the sides of the cube.

Cylinder: The surface area of a cylinder is given by the formula A = 2πr^2 + 2πrh, where r is the radius of the circular base and h is the height of the cylinder.

Sphere: The surface area of a sphere is given by the formula A = 4πr^2, where r is the radius of the sphere.

Cone: The surface area of a cone is given by the formula A = πr^2 + πrs, where r is the radius of the circular base, and s is the slant height of the cone.

Calculating surface area is useful in various real-world situations, such as determining the amount of material needed to cover a particular surface area or calculating the amount of heat transfer from an object.

Solved Examples of Surface area

Find the surface area of a rectangular prism with dimensions of 4 meters by 5 meters by 6 meters.
Solution: Using the formula A = 2lw + 2lh + 2wh, we have A = 2(4 x 5) + 2(4 x 6) + 2(5 x 6) = 148 square meters. Therefore, the surface area of the rectangular prism is 94 square meters.

Find the surface area of a cube with a side length of 3 centimeters.
Solution: Using the formula A = 6s^2, we have A = 6(3^2) = 54 square centimeters. Therefore, the surface area of the cube is 54 square centimeters.

Find the surface area of a cylinder with a radius of 2 meters and a height of 8 meters.
Solution: Using the formula A = 2πr^2 + 2πrh, we have A = 2π(2^2) + 2π(2 x 8) = 40π square meters (approx. 125.66 square meters). Therefore, the surface area of the cylinder is 40π square meters.

Find the surface area of a sphere with a radius of 5 inches.
Solution: Using the formula A = 4πr^2, we have A = 4π(5^2) = 100π square inches (approx. 314.16 square inches). Therefore, the surface area of the sphere is 100π square inches.

Find the surface area of a cone with a radius of 3 centimeters and a slant height of 6 centimeters.
Solution: Using the formula A = πr^2 + πrs, we have A = π(3^2) + π(3 x 6) = 27π square centimeter ( Approx. 84.82 square centimeter). Therefore, the surface area of the cone is 27π square centimeters.

Polyhedra

Polyhedra are three-dimensional figures that consist of flat polygonal faces, straight edges, and sharp corners or vertices. Examples of polyhedra include cubes, prisms, pyramids, and dodecahedrons.

The study of polyhedra is a branch of geometry known as solid geometry. Polyhedra are classified according to the number of faces, edges, and vertices they have. For example, a cube has six faces, 12 edges, and eight vertices.

Polyhedra are important in many fields, including mathematics, engineering, and architecture. They can be used to model and analyze structures and systems, such as crystals, molecules, and architectural designs.

There are several types of polyhedra, including:

Regular polyhedra: These are polyhedra whose faces are congruent regular polygons, and where the same number of faces meet at each vertex. There are only five regular polyhedra, known as the Platonic solids: tetrahedron, cube, octahedron, dodecahedron, and icosahedron.

Convex polyhedra: These are polyhedra whose faces all lie on one side of a plane passing through each face. A convex polyhedron is one that does not have any internal angles greater than 180 degrees.

Non-convex polyhedra: These are polyhedra whose faces intersect each other or have internal angles greater than 180 degrees. Non-convex polyhedra can be further classified as concave or star polyhedra.

Regular-faced polyhedra: These are polyhedra whose faces are congruent but not necessarily regular polygons. They include the Archimedean solids, which are composed of regular polygons of two or more types.

Polyhedra have many interesting properties, such as Euler’s formula, which relates the number of faces, edges, and vertices of a polyhedron. They are also used in topology, which is the study of the properties of objects that remain the same even when they are stretched, twisted, or bent.

Solved Examples of Polyhedra

Find the number of edges of a cube.
Solution: A cube has six faces, and each face is a square. Since a square has four edges, the cube has 4 x 6 = 12 edges.

Find the number of vertices of a dodecahedron.
Solution: A dodecahedron has 12 faces, and each face is a regular pentagon. Each vertex of the dodecahedron is the intersection of three faces. Each face has five vertices, so the total number of vertices in the dodecahedron is (12 x 5) / 3 = 20.

Find the number of faces of a triangular prism.
Solution: A triangular prism has two triangular faces and three rectangular faces. Therefore, it has 2 + 3 = 5 faces.

Find the surface area of a regular tetrahedron with edge length 5 cm.
Solution: A regular tetrahedron has four equilateral triangle faces. The area of an equilateral triangle with edge length 5 cm is given by (sqrt(3) / 4) x (5)^2 = (25 sqrt(3)) / 4 cm^2. Therefore, the surface area of the tetrahedron is 4 x (25 sqrt(3)) / 4 = 25 sqrt(3) cm^2.

Find the volume of a cube with edge length 8 cm.
Solution: The volume of a cube is given by V = s^3, where s is the length of a side. Therefore, the volume of the cube is 8^3 = 512 cubic cm.

Solid Geometry FAQS

Grade 8 Science Worksheets

• Earth & Space Science
• Physical Science
• Life Science
• Chemistry
• Structure of Atom (Basic)
• Fossils
• Bio Classification
• Sedimentary Rock
• Chemical Reaction
• Climate
• Compounds and Mixtures
• The Universe
• Dynamics of our solar system
• Organization of the universe, and its development
• Earth Systems
• Rocks and Fossils
• Sources of energy that power the subsystems and cycles of the dynamic earth: the geosphere, hydrosphere, atmosphere and biosphere
• Heredity
• Evolutionary Theory
• Structure and function of the cell.
• Chromosomes, genes, and the molecular basis of heredity
• Interdependence of organisms and their interaction with the physical environment
• Behavior of animals
• Understanding biological evolution
• How Living things are classified
• How Living Systems live
• Life Cycle of living things
• Structure of the atom
• States and properties of matter
• Changes in States Of Matter
• Chemical properties of Matter
• Structure of matter
• Conservation of matter
• Basics of chemical reactions
• Forces and Motion
• Laws and Formulas Of Motion

Grade 8 Math Worksheets

• Rational & Irrational Numbers
• Prime Factorization
• Comparing Inetgers
• Exponent Rules
• Ratios and Proportions
• Permutations and Combinations
• Scientific Notation
• Linear Functions
• Percents
• Variable Expressions