Indefinite Integrals
Now, if we are given the velocity of an object at any time i.e. any given instant, can we determine the displacement of that object at that instant.
Similarly, the rate of change of velocity is acceleration. If acceleration at any given time is known to us, can we identify its velocity?
Differentiation helps us to find the rate of change of any quantity with respect to another. Similarly, we need to reverse the process to find the answers to the above questions.
The answers to these questions can be given by what is called Integration.
Figure 1: https://commons.wikimedia.org/wiki/File:Terminal_Velocity.png
Here, we introduce the concept of Integration.
- Integration is the inverse process of differentiation.
- In Differentiation, we are given a function f(x) & we find its derivative i.e. f ‘ (x).
- In Integration, we are given the derivative f ‘ (x) of a function f(x). We have to find the original function i.e. f(x) or the anti derivative.
This process is called anti or Integration.
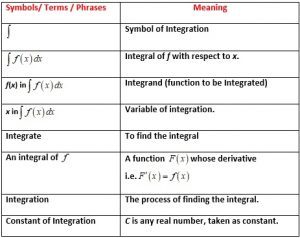
Indefinite Integral
Let F(x) be function which is differentiable in an interval, I. f(x) is a function such
that (F(x))= F ‘(x)=f(x), x
I . Then we have,
f(x) dx = F(x) where,
f(x)dx denotes the family or class of anti derivatives which is read as Indefinite integral of f with respect to x.
Note: C is a constant called the Constant of Integration.
For every distinct value of C, we get a different member of the family. Hence, it is called Indefinite (which is not fixed/certain) integral.

Properties of Indefinite Integrals
-
f ‘ (x)dx= f(x)+C
[f(x)+g(x)]dx =
f(x)dx +
g(x)dx
[f(x)-g(x)]dx =
f(x)dx –
g(x)dx
kf(x)dx = k
f(x)dx + C, where k is any non zero real number.
- .
[
f(x) +
g(x)]dx =
f(x)dx +
g(x)dx .
Examples
Now let’s consider some examples on indefinite integrals.
Example 1: Find the anti-derivative i.e. Integral of f(x) = + 3x with respect to x.
(
+ 3x)dx =
(
)dx + 3
(
)dx
= +3
+C =
+ 3
+C
where C is the constant of Integration.
Example 2: Evaluate:(7Sin x – 3Cos x)dx
(7Sin x-3Cos x)dx = 7
Sin xdx – 3
Cos xdx
= 7(-Cos x) – 3(Sin x) +C = -7Cos x – 3Sin x+C
Example 3: Evaluate: dx .
dx =
dx
=
dx –
dx =
– log|x|+ C =
– log|x|+C
Example 4: Evaluate: dx
dx =
dx
= (3
x + 4CosecxCotx)dx =3
xdx+4
CosecxCotxdx .
= -3Cotx -4Cosecx + C
Example 5: Evaluate: (3
-2Sin x+7
)dx
(3
-2Sin x+7
)dx
=3 dx -2
Sin xdx+7
dx=3
-2(-Cosx) +7
+C
=+2Cosx +
+C=
+ 2Cosx+
x
+C
Check Point
Evaluate the following Integrals –
(15
+20)dx
(7Cosx – 3
)dx
(7
+ 34
+17)dx
(x-1)(x-2)dx
dx
Answer Key
(15
+20)dx=
+ 20x +C
(7Cosx – 3
)dx = 7Sin x – 3Tan x+C
(7
+ 34
+17)dx = 7
+2
+17x+C
(x-1)(x-2)dx=
–
+ 2x + C
dx =
– 2
+C .
Personalized Online Tutoring
eTutorWorld offers affordable one-on-one live tutoring over the web for Grades 2-12, Test Prep help for Standardized tests like SCAT, CogAT, SSAT, SAT, ACT, ISEE and AP. You may schedule online tutoring lessons at your personal scheduled times, all with a Money-Back Guarantee. The first one-on-one online tutoring lesson is always FREE, no purchase obligation, no credit card required.
For answers/solutions to any question or to learn concepts, take a FREE Demo Session.
No credit card required, no obligation to purchase.
Just schedule a FREE Sessions to meet a tutor and get help on any topic you want!
Pricing for Online Tutoring
| Tutoring Package | Validity | Grade (1-12), College |
|---|---|---|
| 5 sessions | 1 Month | $139 |
| 1 session | 1 Month | $28 |
| 10 sessions | 3 months | $269 |
| 15 sessions | 3 months | $399 |
| 20 sessions | 4 months | $499 |
| 50 sessions | 6 months | $1189 |
| 100 sessions | 12 months | $2249 |
IN THE NEWS

Our mission is to provide high quality online tutoring services, using state of the art Internet technology, to school students worldwide.
Online test prep and practice
SCAT
CogAT
SSAT
ISEE
PSAT
SAT
ACT
AP Exam
Science Tutoring
Physics Tutoring
Chemistry Tutoring
Biology Tutoring
Math Tutoring
Pre-Algebra Tutoring
Algebra Tutoring
Pre Calculus Tutoring
Calculus Tutoring
Geometry Tutoring
Trigonometry Tutoring
Statistics Tutoring
Quick links
Free Worksheets
Fact sheet
Sales Partner Opportunities
Parents
Passive Fundraising
Virtual Fundraising
Our Expert Tutors
Safe and Secure Tutoring
Interactive Online Tutoring
After School Tutoring
Elementary School Tutoring
Middle School Tutoring
High School Tutoring
Home Work Help
Math Tutors New York City
Press
©2022 eTutorWorld Terms of use Privacy Policy Site by Little Red Bird
©2022 eTutorWorld
Terms of use
Privacy Policy
Site by Little Red Bird






