Equation of a Line

The equation of a line is a linear relation between two variables x and y, which is satisfied by the coordinates of each & every point on the line and not by any other point.

There are various forms of Equation of a line.

Example:

1. 2x + 3y + 7 = 0 which can also be written as 2x + 3y = (-7).
2. 4x + 3 = 7 where B = 0.
3. 3y + 2 = 5 where A = 0.

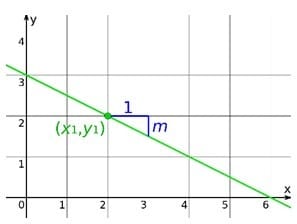
Point Slope Form

Equation of a line with slope or gradient m and passing through the point (,) is given by

( – ) =  ( – )

Example:

1. Equation of line passing from origin (0, 0) and slope 1 is (y – 0) = (x – 0) or y = x.
2. Equation of line passing from (1, 3) and slope 4 is (y – 3) = 4(x – 1) or y – 3 = 4x – 4

Hence the line is given by the equation 4x – y – 1 = 0.

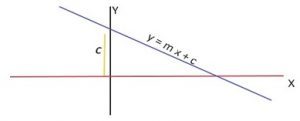
Slope Intercept form

The length of the intercept made by of a line on the Y-axis is called its y-intercept.

Equation of a line with slope or gradient m and making an y intercept of c units is given

by                                         (y – c) = m ( x – 0 )

i.e                                            y=mx + c

Example:

1. Equation of line with slope, m =  &  y-intercept c = 7 is y = x + 7.
2. Equation of line with slope, m = 11 & y-intercept c = -2 is y = 11x – 2.

1. Write the equation of the line 3x = 4y + 7 in general form.
2. Convert the equation 3x = 4y + 2 in slope intercept form.
3. Find the equation of the line passing from origin (0, 0) and slope 4.
4. Find the equation of the line passing from origin (1, 5) and slope -7.
5. Find the equation of the line with slope 2 & y-intercept 11.
6. Find the equation of the line with slope & y-intercept -5.

Answer Key

1. 3x – 4y – 7 = 0.
2. Y =  x –
3. y = 4x
4. 7x + y – 12 = 0.
5. y = 2x + 11
6. y = x – 5 or 3x – 7y – 35=0.