Slope-intercept Equation of a Line using two points

Since we have already discussed the slope intercept form of the equation of a line.

Substituting the value of m from above equation we have(y – ) =  ( – ),

which can be written as y= (x-)+

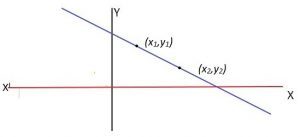
Example

1.  Find the equation of line passing through (2, 1) and (7, 2).Here slope m=  = =Substitute the value of m from above we have(y-5)=(x-2)or y=x−+1=x+ which is the slope intercept form obtained using two points.
2. Find the equation of line passing through (3, 0) and (5, 8).Here slope m= = =  = 4Substitute the value of m from above we have (y – 0) = 4(x – 3) = 4x – 12or y = 4x – 12.                                      

CHECK POINT

1. Find the equation of a line passing through (5, 3) & (-5, -3).
2. Find the equation of a line passing through (2, 4) & (0, 6) in slope intercept form.
3. Find the equation of a line passing through (15, 9) & (9, 15) in slope intercept form.
4. Find the equation of a line passing through (0, 3) & (11, -7) in slope intercept form.
5. Find the equation of a line passing through (0, 0) & (12, 23) in slope intercept form.