Domain, Range & Functions
Calculus Worksheet
Have you ever inflated a spherical balloon?
What do we observe? As we start inflating the balloon its radius starts increasing and consequently its volume also starts increasing.
Volume of the spherical balloon is given by V = .
Here Volume V (dependent variable) is a function of radius r (independent variable).
Hence, we introduce the concept of Function.
I. Function
If A & B are any two nonempty sets. Then a function f from A to B is a rule or correspondence that assigns to each element of set A, one and only one element of B.
A function from A to B is denoted by f: AB where y = f(x),
.
If y = f(x), the we say that y is the image of x under f
and is the pre-image of y under f.
II. Domain, Range & Co-domain of a Function.
If f: AB is a function from set A to set B, then set A is called the Domain of f and set B is called the co-domain of f. The set of all images of the elements of set A is called the Range of f.
III. Real valued function: A function f: AB is called a real valued function, if its co-domain B is a subset of the set of real numbers.
Real function: If A & B both are subsets of real numbers, then f: A B is called a Real function.
IV. Algebra of Functions:
If f: AR and g: A
R are any two functions then
![]() we have:
we have:
- (f+g)(x)=f(x)+g(x)
- (f-g)(x)=f(x)-g(x)
- (f.g)(x)=f(x).g(x)
=
, g(x)
0.
- (cf)(x)=cf(x), where ‘c’ is a any real number
Note: The value of f(x) at x = a is denoted by f(a) and it is obtained by replacing, that is, substituting x with a.
Examples
Now let’s consider some examples on functions.
Example 1: Find the value of at at x = 1 .
Value of f(x) at (x=1)= f(1)=+ 3(1)=1+3=4.
Example 2: If f(x)= and g(x)=x+1 then find (f+g),(f-g) ,(f.g) &
.
(f+g)(x)=f(x)+g(x)=+(x+1)=
+1.
(f-g)(x)=f(x)-g(x)=-(x+1)=
-1-1.
(f.g)(x)=f(x).g(x)=(x+1)=
+
.
(x)=
=
,g(x)=(x+1)
0.
Example 3: Find the value of f(5)& 3 f(x) if f(x)= .
f(x)=
f(5)==
=
3f(x)=3[f(x)]=3=
Check Point
- Find the value of at f(x) =
+20x at x=2.
- Find the value of at f(x) =
+2
-6x-9 at x = -1.
- Find the value of f(2) if f(x) =
.
- If f(x)=(x+2)&g(x)=(x-2) then find(f+g) ,(f-g) ,(f.g) &
.
- If f(x)=
+2x+3& g(x)= (
-3) then find (f+g), (f-g), (f.g)&
.
Answer Key
- 56
- -4
- f(2)=
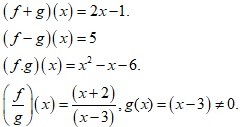
5.
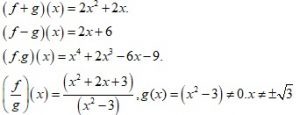
eTutorWorld Understands Math Tutoring | Online Math Worksheets are Important Tools
Understanding graphs, charts, and opinion polls in a newspaper, for calculating house and car payments, and for choosing a long-distance telephone service are impossible without strong math skills …and the only way to develop strong math skills is by constant practice.
‘Practice makes a man perfect’ holds true for no other field better than for math. A middle or high school student must set aside a minimum of an hour for math every day. Other than textbooks, worksheets help you revise and understand concepts better.
Our expert tutors prepare online maths worksheets that are age and grade-appropriate. Grade-wise math worksheets for Elementary Math, Arithmetic, Pre-Algebra, Algebra, Geometry, Trigonometry, Statistics, Pre-Calculus and Calculus can be solved to improve math skills, to get ahead or to even catch up.
You may download these FREE online math worksheets in the PDF format, and then print and email us their solutions for a free evaluation and analysis by eTutorworld’smath expert tutors.
You may solve these worksheets by yourself or with your peers while studying together.
The Answer Key at the end of each worksheet allows for a self-evaluation.
Personalized Online Tutoring
eTutorWorld offers affordable one-on-one live tutoring over the web for Grades K-12, Test Prep help for Standardized tests like SCAT, CogAT, MAP, SSAT, SAT, ACT, ISEE and AP. You may schedule online tutoring lessons at your personal scheduled times, all with a Money-Back Guarantee. The first one-on-one online tutoring lesson is always FREE, no purchase obligation, no credit card required.
For answers/solutions to any question or to learn concepts, take a FREE CLASS.
No credit card required, no obligation to purchase.
Just book a free class to meet a tutor and get help on any topic you want!
Pricing for Online Tutoring
| Tutoring Package | Validity | Grade (1-12), College |
|---|---|---|
| 5 sessions | 1 Month | $139 |
| 1 session | 1 Month | $28 |
| 10 sessions | 3 months | $269 |
| 15 sessions | 3 months | $399 |
| 20 sessions | 4 months | $499 |
| 50 sessions | 6 months | $1189 |
| 100 sessions | 12 months | $2249 |
IN THE NEWS

Our mission is to provide high quality online tutoring services, using state of the art Internet technology, to school students worldwide.
Online test prep and practice
SCAT
CogAT
SSAT
ISEE
PSAT
SAT
ACT
AP Exam
Science Tutoring
Physics Tutoring
Chemistry Tutoring
Biology Tutoring
Math Tutoring
Pre-Algebra Tutoring
Algebra Tutoring
Pre Calculus Tutoring
Calculus Tutoring
Geometry Tutoring
Trigonometry Tutoring
Statistics Tutoring
Quick links
Free Worksheets
Fact sheet
Sales Partner Opportunities
Parents
Passive Fundraising
Virtual Fundraising
Our Expert Tutors
Safe and Secure Tutoring
Interactive Online Tutoring
After School Tutoring
Elementary School Tutoring
Middle School Tutoring
High School Tutoring
Home Work Help
Math Tutors New York City
Press
©2022 eTutorWorld Terms of use Privacy Policy Site by Little Red Bird
©2022 eTutorWorld
Terms of use
Privacy Policy
Site by Little Red Bird







