Online Trigonometry Tutoring: Laws of sines & cosines
Relationship between the angles and the side lengths of triangle
Simplify trigonometry. Our expert and qualified trigonometry tutors understand your problems and guide you towards better grades in trigonometry. Our aim is to help the student understand concepts in trigonometry and master the techniques of solving problems quickly with confidence.
Learn the laws of sines and cosines from certified online trigonometry tutor
✓ It states that “When we divide side a by the sine of angle A, it is equal to side b divided by the
sine of angle B, and also equal to side c divided by the sine of angle C”.
✓ It can be used to –
Calculate the unknown sides (Triangulation)
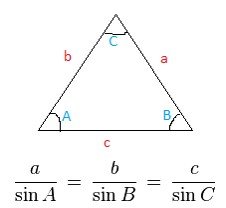
✓ Angles of a Triangle Law can be applied if
- SSA – two sides and angle not included between them are given
- ASA – two angles and side between them are given
- SAS – two angles and one side that is not included in the angles

What is the Law of Cosines
Relationship between the side lengths and the angles of a triangle
The Law of Cosines can be given as
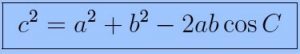
Other two versions of Law of Cosines are:
a2 = b2 + c2 – 2 bc cos A
b2 = a2 + c2 – 2ac cos B
What are the Uses of Laws of Cosines?
The Laws of Cosines is used:
- To find the 3rd side of a triangle when we know the 2 sides and the angle between them (SAS)
- To find the angles of a triangle when we know all the 3 sides (SSS) of triangle.
When should we use the Laws of Sines?
1.If you are given: Angle-Side-Angle (ASA) or Angle-Angle-Side (AAS). OR
2.If you are given: Hypotenuse-Leg (HL), you have a right triangle. OR
3.If you are given: Side-Side-Angle (SSA– in that order!!), then you have the AMBIGUOUS CASE ( we’ll discuss this case after the examples)
Example 1:
In a triangle ABC, a = 10, b = 5, and ∠A = 45°. Find the value of ∠B.
a/sin A = b/sin B
10/sin 45 = 5/sin B
sin B = 1/2√2 or √2/4 (because sin 45 = 1/√2)
sin B = 0.3535
B = sin-1(0.3535) = 20.7
Example 2:
In triangle ABC, side b = 5 cm, c = 10 cm, and the angle at A is 60°. Find side a.
According to law of cosines, a2 = b2 + c2 – 2bc cos 60
a2 = 52 + 102 – 2 x 5 x 10 cos 60
a2 = 125 – 2 x 5 x 10 x ½ (cos 60 = ½)
= 125 – 50
a2 = 75
a = √75
Ambiguous Case – Law of Sines
There are 5 situations when we need to use the Ambigious Case of the Law of Sines:
Case I: Angle is acute.
Side ‘a’ may or may not be long enough
to reach side ‘c’. We calculate the height
of the altitude from angle C to side c to
compare it with side a.
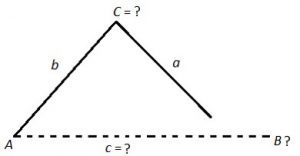
Using Case I: First, use SOH-CAH-TOA to find h:
sinA =
h = bsin A
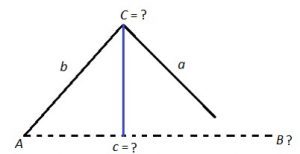
Then, compare ‘h’ to sides a and b . . .
Case I: If a < h, then NO triangle exists with these dimensions.
sinA =
h = bsin A

Then, compare ‘h’ to sides a and b . .
Case II: If h < a < b, then TWO triangles exist with these dimensions.

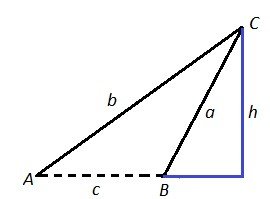
If we open side ‘a’ to the outside of h, If we open side ‘a’ to the inside of h, angle B is obtuse.
angle B is acute.
Case III: If h < b < a, then ONE triangle exists with these dimensions.
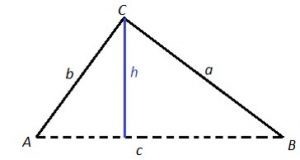
Since side a is greater than side b, side a cannot open to the inside of h, it can only open to the outside, so there is only 1 triangle possible!
Case IV: If h = a, then ONE triangle exists with these dimensions.
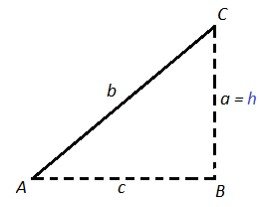
If a = h, then angle B must be a right angle and there is only one possible triangle with these dimensions.
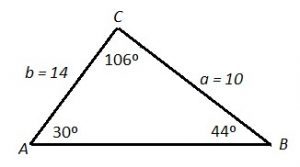
Given a triangle with angle A = 30°, side a = 14 cm and side b = 15 cm, find the other dimensions.
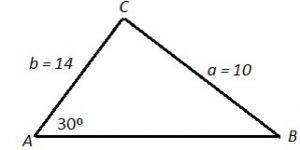
Using Law of Sines, =
=
10sinB = 14 sin30
sinB = = 0.7
B = (0.7) = 44.42 ≅ 44
Angles could be 30°, 44°, and 106°: sum 180°.
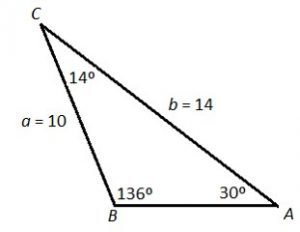
The angle from Quadrant II could create angles 30°, 14°, and 136°: sum 180°.
Check Point
Problem 1. A = 40; B = 20; a = 2. Find side b.
Problem 2. If b = 5, c = 2, A = 30, find a.
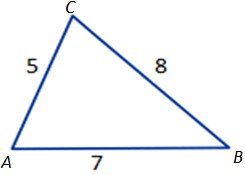
Problem 3. Given ABC, a = 8, b = 5,c = 7, find C using law of cosines.
Answer Key
- b = 3.76 approx
- a = 3.42 approx
- C = 60 degrees
Personalized Online Tutoring
eTutorWorld offers affordable one-on-one live tutoring over the web for Grades 2-12, Test Prep help for Standardized tests like SCAT, CogAT, SSAT, SAT, ACT, ISEE and AP. You may schedule online tutoring lessons at your personal scheduled times, all with a Money-Back Guarantee. The first one-on-one online tutoring lesson is always FREE, no purchase obligation, no credit card required.
For answers/solutions to any question or to learn concepts, take a FREE Demo Session.
No credit card required, no obligation to purchase.
Just schedule a FREE Sessions to meet a tutor and get help on any topic you want!
Pricing for Online Tutoring
| Tutoring Package | Validity | Grade (1-12), College |
|---|---|---|
| 5 sessions | 1 Month | $139 |
| 1 session | 1 Month | $28 |
| 10 sessions | 3 months | $269 |
| 15 sessions | 3 months | $399 |
| 20 sessions | 4 months | $499 |
| 50 sessions | 6 months | $1189 |
| 100 sessions | 12 months | $2249 |
IN THE NEWS

Our mission is to provide high quality online tutoring services, using state of the art Internet technology, to school students worldwide.
Online test prep and practice
SCAT
CogAT
SSAT
ISEE
PSAT
SAT
ACT
AP Exam
Science Tutoring
Physics Tutoring
Chemistry Tutoring
Biology Tutoring
Math Tutoring
Pre-Algebra Tutoring
Algebra Tutoring
Pre Calculus Tutoring
Calculus Tutoring
Geometry Tutoring
Trigonometry Tutoring
Statistics Tutoring
Quick links
Free Worksheets
Fact sheet
Sales Partner Opportunities
Parents
Passive Fundraising
Virtual Fundraising
Our Expert Tutors
Safe and Secure Tutoring
Interactive Online Tutoring
After School Tutoring
Elementary School Tutoring
Middle School Tutoring
High School Tutoring
Home Work Help
Math Tutors New York City
Press
©2022 eTutorWorld Terms of use Privacy Policy Site by Little Red Bird
©2022 eTutorWorld
Terms of use
Privacy Policy
Site by Little Red Bird






