Parallel and Perpendicular Lines in Graphs of Linear Equations
A Linear equation is an equation in which the highest exponent of the variable present in the equation is one. When we draw the graph of the linear equation, it forms a straight line.
If any two lines in the plane are drawn, they are either parallel or intersecting.
How do you know if a line is parallel?
Two lines are parallel if their slopes are equal.
Hence the lines y = m1x + c1 and y = m2x + c2 are parallel if m1 = m2.
In fact, two parallel lines differ by a constant.
Hence if the equation of line is y = mx + c, then, equation of a line parallel to it is y = mx + k, where k is a constant. To find the particular line, we require a unique value of k. For this additional condition is given.
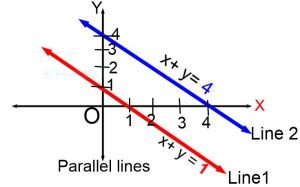
Using the above concept, the equation of a line parallel to above line is y = 7x + k, where k is any real number.
Example 2: Write the equation of a line parallel to y = 7x + 10 which passes from (1, 1).
The equation of a required line parallel to above line is y = 7x + k, where k is any real number.
Since the above line passes from (1, 1), hence it satisfies the required equation y = 7x + k.
Hence, 1 = 7(1) + k and k = 1 – 7 = -6.
Hence, the required equation is y = 7x – 6.
How do you know if a line is perpendicular?
Two lines are perpendicular if the product of their slopes is -1.
Hence the lines y = m1x + c1 and y = m2x + c2 are perpendicular if m1m2 = -1 or m1 =
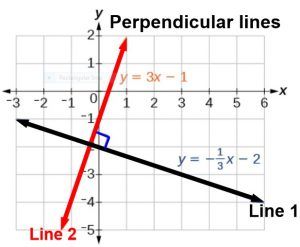
Comparing with the slope intercept form, y = mx + c, the slope of given line is m = 2. Hence, the slope of a line perpendicular to given line is –= –
.
Equation of line perpendicular to given line is y= – x + k = –
x+k, where k is any real number.
Example 4: Find the equation of a line perpendicular to y = 3x + 5 passing from (1, 2).
As, done in the previous example slope of given line is m = 3.
Hence, the slope of a line perpendicular to given line is – = –
.
Equation of line passing from (1, 2) and slope – is (y – 2) = –
(x-1)
3(y – 2) = -(x – 1)
3y – 6 = –x + 1
x + 3y = 7
Note:
(1) If two lines are parallel,then their slopes are equal.
(2) If two lines are perpendicular,then product of their slopes is -1.
To find the slope of a line perpendicular to given line,We take the reciprocal and change its sign.
Hence,slope of a line perpendicular to a given line with slope m is -1/m.
Comparing with the slope intercept form, y = mx + c
The slope of first line, y = (-1)x + 10 is m1 = -1.
The slope of second line, y = (-1)x + 100 is m2 = -1.
m1 = m2 = -1. Hence the given lines are parallel.
Example 6: Check whether the lines x + y = 10 and x – y = 100 are parallel or perpendicular.
Comparing with the slope intercept form, y = mx + c
The slope of first line, y = (-1)x + 10 is m1 = -1.
The slope of second line, y = (1)x – 100 is m2 = 1.
m1 m2 = -1, so the given lines are perpendicular.
Check Point
- Find the equation of the line passing through (-1, 5) & parallel to the line y = 5x + 1.
- Find the equation of the line passing through (-1, 5) & perpendicular to the line y = 5x + 1.
- Check whether the lines, 3x + y = 15 and 21x + 7y = 28 are parallel or perpendicular.
- Check whether the lines 3x + y = 15 and x – 3y = 28 are parallel or perpendicular.
- Find the equation of the line parallel to the line, y = 7x + 51.
- Find the equation of the line perpendicular to the line y = 7x + 51.
Answer Key
- The required parallel line is y = 5x + 10.
- The required perpendicular line is y = –
x +
or x + 5y = 26.
- Since, slopes of the two lines are equal which is -3. Hence the given lines are parallel.
- Since, product of the slopes of the two lines is -1. Hence the given lines are perpendicular.
- The equation of the line parallel to the line y = 7x + 51 is y = 7x + k, where k is any real
- The equation of the line perpendicular to the line y = 7x + 51 is y = –
x + k , where k is any real
Personalized Online Tutoring
eTutorWorld offers affordable one-on-one live tutoring over the web for Grades 2-12, Test Prep help for Standardized tests like SCAT, CogAT, SSAT, SAT, ACT, ISEE and AP. You may schedule online tutoring lessons at your personal scheduled times, all with a Money-Back Guarantee. The first one-on-one online tutoring lesson is always FREE, no purchase obligation, no credit card required.
For answers/solutions to any question or to learn concepts, take a FREE Demo Session.
No credit card required, no obligation to purchase.
Just schedule a FREE Sessions to meet a tutor and get help on any topic you want!
Pricing for Online Tutoring
| Tutoring Package | Validity | Grade (1-12), College |
|---|---|---|
| 5 sessions | 1 Month | $139 |
| 1 session | 1 Month | $28 |
| 10 sessions | 3 months | $269 |
| 15 sessions | 3 months | $399 |
| 20 sessions | 4 months | $499 |
| 50 sessions | 6 months | $1189 |
| 100 sessions | 12 months | $2249 |
IN THE NEWS

Our mission is to provide high quality online tutoring services, using state of the art Internet technology, to school students worldwide.
Online test prep and practice
SCAT
CogAT
SSAT
ISEE
PSAT
SAT
ACT
AP Exam
Science Tutoring
Physics Tutoring
Chemistry Tutoring
Biology Tutoring
Math Tutoring
Pre-Algebra Tutoring
Algebra Tutoring
Pre Calculus Tutoring
Calculus Tutoring
Geometry Tutoring
Trigonometry Tutoring
Statistics Tutoring
Quick links
Free Worksheets
Fact sheet
Sales Partner Opportunities
Parents
Passive Fundraising
Virtual Fundraising
Our Expert Tutors
Safe and Secure Tutoring
Interactive Online Tutoring
After School Tutoring
Elementary School Tutoring
Middle School Tutoring
High School Tutoring
Home Work Help
Math Tutors New York City
Press
©2022 eTutorWorld Terms of use Privacy Policy Site by Little Red Bird
©2022 eTutorWorld
Terms of use
Privacy Policy
Site by Little Red Bird






