Binomial Theorem
Binomial theorem is a theorem developed for calculating any power of any binomial without actually multiplying at length.
General binomial expansion is denoted by
(a+b)n =nc0an +nc1an-1b+nc2an-2b2+…………………..+ncn-1abn-1+ncnbn where n>=0 and
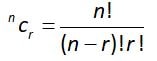
Example – (x+y)3=3c0x3+3c1x2y+3c2xy2+3c2y3
Example – Expand (p+1)3
(p+1)3=3c0*p3+3c1*p2*1+3c2*p*12+3c2*13
= p3+3p2+3p+1
Some Facts about Binomial Theorem
- General term for an expansion (a+b)n is Tr+1 =ncran-rbr is , where 0 <= r<= n.
- Number of terms in expansion will be n + 1.
Check Point:
Expand the following binomials –
1) (a+b)3
2) (s+3)3
3) (y2+1)4
4) (3+x)4
5) (z+2)6
Answer Key
1) a3+3a2b+3b2a+b3
2) s3+9s2+27s+27
3) y8+4y6+6y4+4y2+1
4) 81+108x+54x2+12x3+x4
5) z6+12z5+60z4+160z3+240z2+192z+64
Personalized Online Tutoring
eTutorWorld offers affordable one-on-one live tutoring over the web for Grades 2-12, Test Prep help for Standardized tests like SCAT, CogAT, SSAT, SAT, ACT, ISEE and AP. You may schedule online tutoring lessons at your personal scheduled times, all with a Money-Back Guarantee. The first one-on-one online tutoring lesson is always FREE, no purchase obligation, no credit card required.
For answers/solutions to any question or to learn concepts, take a FREE Demo Session.
No credit card required, no obligation to purchase.
Just schedule a FREE Sessions to meet a tutor and get help on any topic you want!
Pricing for Online Tutoring
| Tutoring Package | Validity | Grade (1-12), College |
|---|---|---|
| 5 sessions | 1 Month | $139 |
| 1 session | 1 Month | $28 |
| 10 sessions | 3 months | $269 |
| 15 sessions | 3 months | $399 |
| 20 sessions | 4 months | $499 |
| 50 sessions | 6 months | $1189 |
| 100 sessions | 12 months | $2249 |
IN THE NEWS

Our mission is to provide high quality online tutoring services, using state of the art Internet technology, to school students worldwide.
Online test prep and practice
SCAT
CogAT
SSAT
ISEE
PSAT
SAT
ACT
AP Exam
Science Tutoring
Physics Tutoring
Chemistry Tutoring
Biology Tutoring
Math Tutoring
Pre-Algebra Tutoring
Algebra Tutoring
Pre Calculus Tutoring
Calculus Tutoring
Geometry Tutoring
Trigonometry Tutoring
Statistics Tutoring
Quick links
Free Worksheets
Fact sheet
Sales Partner Opportunities
Parents
Passive Fundraising
Virtual Fundraising
Our Expert Tutors
Safe and Secure Tutoring
Interactive Online Tutoring
After School Tutoring
Elementary School Tutoring
Middle School Tutoring
High School Tutoring
Home Work Help
Math Tutors New York City
Press
©2022 eTutorWorld Terms of use Privacy Policy Site by Little Red Bird
©2022 eTutorWorld
Terms of use
Privacy Policy
Site by Little Red Bird






