Solve System of Linear Equations with Elimination and Substitution
Grade 8 Math Worksheets

Schedule a Free session to clear worksheet doubts
No credit card required, no obligation to purchase.
Just schedule a FREE Sessions to meet a tutor and get help on any topic you want!
Let’s see this with the help of an example –
3x – 4y = 11 …Equation (1)
-3x + 2y = -7 …Equation (2)
When we add the two equations, x-terms will be eliminated. This happens because the coefficients of the x-terms, 3 and -3, are opposites of each other.
So, adding we get:
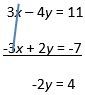
Dividing both sides by -2, we get, y = -2
Now put y = -2 back in equation (1) or equation (2) to get the value of x. Let us put y = -2 in equation (1):
3x – 4(-2) = 11 3x + 8 = 11
3x = 11 – 8 3x = 3
x = 1
Check the solution: Put x = 1 and y = -2 in the given equations to check the answer.
Left Hand Side (L.H.S) of the equation 3x – 4y = 11:
3(1) – 4(-2) = 3 + 8 = 11, which is the same as right Hand Side (R.H.S) of the equation.
Since L.H.S = R.H.S, so the values are correct.
Similarly, L.H.S of the equation -3x + 2y = -7:
-3(1) + 2(-2) = -3 – 4 = -7, which is the same as R.H.S of the equation.
Since L.H.S = R.H.S, so the values are correct.
eTutorWorld Understands Math Tutoring | Online Math Worksheets are Important Tools
Understanding graphs, charts, and opinion polls in a newspaper, for calculating house and car payments, and for choosing a long-distance telephone service are impossible without strong math skills …and the only way to develop strong math skills is by constant practice.
‘Practice makes a man perfect’ holds true for no other field better than for math. A middle or high school student must set aside a minimum of an hour for math every day. Other than textbooks, worksheets help you revise and understand concepts better.
Our expert tutors prepare online maths worksheets that are age and grade-appropriate. Grade-wise math worksheets for Elementary Math, Arithmetic, Pre-Algebra, Algebra, Geometry, Trigonometry, Statistics, Pre-Calculus and Calculus can be solved to improve math skills, to get ahead or to even catch up.
You may download these FREE online math worksheets in the PDF format, and then print and email us their solutions for a free evaluation and analysis by eTutorworld’smath expert tutors.
You may solve these worksheets by yourself or with your peers while studying together.
The Answer Key at the end of each worksheet allows for a self-evaluation.
Personalized Online Tutoring
eTutorWorld offers affordable one-on-one live tutoring over the web for Grades K-12, Test Prep help for Standardized tests like SCAT, CogAT, MAP, SSAT, SAT, ACT, ISEE and AP. You may schedule online tutoring lessons at your personal scheduled times, all with a Money-Back Guarantee. The first one-on-one online tutoring lesson is always FREE, no purchase obligation, no credit card required.
For answers/solutions to any question or to learn concepts, take a FREE CLASS.
No credit card required, no obligation to purchase.
Just book a free class to meet a tutor and get help on any topic you want!
Example: Solve the given system of equations by elimination method –
5x – 4y = 9 …Equation (1)
x – 2y = -3 …Equation (2)
Here we can either multiply equation (2) by 5 so that the coefficient of x in equation (2) is also 5 and then we can subtract both the equations to get the value of y, or we can multiply equation (2) by ‘-2’ and then add the two equations to get the value of x.
Here we multiply equation (2) by -2, and then add the equations –
5x – 4y = 9 …Equation (1) ——————— 5x – 4y = 9 …Equation (1)
x – 2y = -3 …Equation (2) ——————— -2x + 4y = 6 …Equation (2)
Adding the equations we get, 5x – 2x = 9 + 6
3x = 15
Dividing by 3 we get, x = 5
Put this value of x = 5 in any of the two equations to get the value of y, putting x = 5 in equation (2) we get:
5 – 2y = -3
2y = 5 + 3
2y = 8 implies y = 4
Check the solution:
L.H.S of the equation 5x – 4y = 9:
5(5) – 4(4) = 25 – 16 = 9, which is equal to the R.H.S of the equation.
L.H.S of the equation x – 2y = -3:
5 – 2(4) = 5 – 8 = -3, which is equal to the R.H.S of the equation.

Example: Solve the following equations for x and y:
2x + y = 3 …Equation (1)
-5x + y = -4 …Equation (2)
Step 1: From equation (1), y = 3 – 2x
Step 2 and 3: Put y = 3 – 2x in equation (2), –5x + (3 – 2x) = -4
-5x – 2x = -4 – 3
-7x = -7 ⇒ x = 1
Step 4: Put x = 1 in equation (1), y = 3 – 2x
y = 3 – 2(1)
y = 3 – 2
y = 1
Step 5: Check the solution: Put x = 1 and y = 1 in any of the given equations to check the answer.
Left Hand Side (L.H.S) of the equation 2x + y = 3:
2(1) + 1 = 2 + 1 = 3, which is equal to the R.H.S of the equation.
Since L.H.S = R.H.S so, the values are correct.
L.H.S of -5x + y = -4:
-5(1) + 1 = -5 + 1 = -4, which is equal to the R.H.S of the equation.
Since L.H.S = R.H.S so, the values are correct.
Check Point
- Solve by elimination method:
x + y = 1
x – y = 3
- Solve by substitution method:
x + 2y = 2
-4x + 3y = 25
- Solve by elimination method:
2x + 5y = -4
3x – y = 11
- Solve by substitution method:
5x + 2y = 0
x – 3y = 0
- Solve by elimination method:
x = 4y – 2
x = 6y + 8
Answer key
- (2, -1)
- (-4, 3)
- (3, -2)
- (0, 0)
- (-22, -5)
Schedule a Free session to clear worksheet doubts
No credit card required, no obligation to purchase.
Just schedule a FREE Sessions to meet a tutor and get help on any topic you want!
Pricing for Online Tutoring
| Tutoring Package | Validity | Grade (1-12), College |
|---|---|---|
| 5 sessions | 1 Month | $139 |
| 1 session | 1 Month | $28 |
| 10 sessions | 3 months | $269 |
| 15 sessions | 3 months | $399 |
| 20 sessions | 4 months | $499 |
| 50 sessions | 6 months | $1189 |
| 100 sessions | 12 months | $2249 |
IN THE NEWS

Our mission is to provide high quality online tutoring services, using state of the art Internet technology, to school students worldwide.
Online test prep and practice
SCAT
CogAT
SSAT
ISEE
PSAT
SAT
ACT
AP Exam
Science Tutoring
Physics Tutoring
Chemistry Tutoring
Biology Tutoring
Math Tutoring
Pre-Algebra Tutoring
Algebra Tutoring
Pre Calculus Tutoring
Calculus Tutoring
Geometry Tutoring
Trigonometry Tutoring
Statistics Tutoring
Quick links
Free Worksheets
Fact sheet
Sales Partner Opportunities
Parents
Passive Fundraising
Virtual Fundraising
Our Expert Tutors
Safe and Secure Tutoring
Interactive Online Tutoring
After School Tutoring
Elementary School Tutoring
Middle School Tutoring
High School Tutoring
Home Work Help
Math Tutors New York City
Press
©2022 eTutorWorld Terms of use Privacy Policy Site by Little Red Bird
©2022 eTutorWorld
Terms of use
Privacy Policy
Site by Little Red Bird







