Volume & Surface Area of a Cylinder
Grade 6 Math Worksheets
How do you calculate the volume of a cylinder?
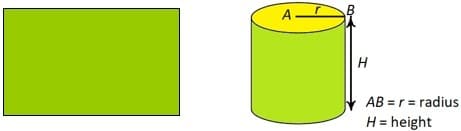
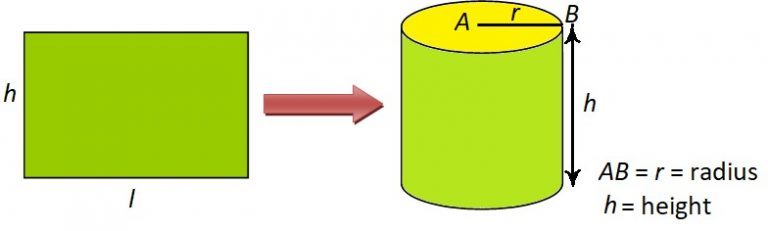
When we roll up a piece of square or rectangular piece of paper, we get a cylinder.
(Note: Diameter is twice the radius)
We measure the area of a circle by using the formula –

When we find the volume of a cylinder, it is 3-dimensional shape, so just the height is multiplied additionally with the area of a circle which is the formula for volume of cylinder.
Volume of a Cylinder
Example: The radius of a cylindrical bottle is 3 cm and length is 7 cm. What is the maximum volume of juice the jar can contain? (Take =
)
Volume =
= × 3 × 3 ×7
=198 cm³

How do you find the surface area of the cylinder?
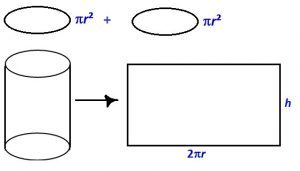
The area of the rectangular sheet of paper is equal to the curved surface area of the cylinder.
The length of the sheet is equal to the circumference of the circular base which is equal to 2r.
So, curved surface area of the cylinder = Area of the rectangular sheet = length × width = perimeter of the base of the cylinder × h = 2rh

Example: Find the surface area of a tube of length 8 cm, diameter 14 cm.
Diameter = 14 cm
So, radius = diameter/2= = 7cm
Curved Surface Area = 2 × ×7 ×8
= 352 cm²

How do you find the total surface area of a cylinder?
As discussed earlier, a cylinder is something which looks like a rolled up rectangle.
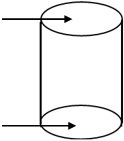
Now to calculate the TSA, we are left with two circles on the top and the bottom.
Area of the circle on top and the base circle when the cylinder is closed on both ends.

Example: Find the total surface area of a cylinder with closed top and bottom which has a radius of 7 cm and height 5 cm.
Hence the total surface area is = {2 × × 7 × 5} + {2 ×
× 7 × 7}
= 220 + 308
Total Surface Area of the cylinder = 528 cm2
Check Point
- What is the volume of cylinder witch height 8 cm and total surface area 1936 cm2? (Take
=
)
- Mark has a kiosk for lemonade at his school fair and has a cylindrical vessel which is of height 21 cm and radius of 4 cm. What volume of lemonade does he need to make to fill his vessel? (Take
=
)
- A cylinder is of height 49 cm is having radius of 5 cm. Find the curved surface area of the cylinder. (Take
=
)
4. How much volume of coffee does a cylindrical thermos of diameter 10 cm and height 14 cm hold? (Take =
)

- Find the height of a cylindrical vessel of curved surface area 1320 mm² and radius 14 mm. (Take
=
)
- What is the height of a pipe with closed valves on both ends which has a total surface area of 8800 cm² and radius of 14 cm? (Take
=
)
Answer key
- 4928 cm³
- 1056 cm³
- 1540 cm²
- 1100 cm²
- 15 mm
- 86 cm
Personalized Online Tutoring
eTutorWorld offers affordable one-on-one live tutoring over the web for Grades 2-12, Test Prep help for Standardized tests like SCAT, CogAT, SSAT, SAT, ACT, ISEE and AP. You may schedule online tutoring lessons at your personal scheduled times, all with a Money-Back Guarantee. The first one-on-one online tutoring lesson is always FREE, no purchase obligation, no credit card required.
For answers/solutions to any question or to learn concepts, take a FREE Demo Session.
No credit card required, no obligation to purchase.
Just schedule a FREE Sessions to meet a tutor and get help on any topic you want!
Pricing for Online Tutoring
| Tutoring Package | Validity | Grade (1-12), College |
|---|---|---|
| 5 sessions | 1 Month | $139 |
| 1 session | 1 Month | $28 |
| 10 sessions | 3 months | $269 |
| 15 sessions | 3 months | $399 |
| 20 sessions | 4 months | $499 |
| 50 sessions | 6 months | $1189 |
| 100 sessions | 12 months | $2249 |
IN THE NEWS

Our mission is to provide high quality online tutoring services, using state of the art Internet technology, to school students worldwide.
Online test prep and practice
SCAT
CogAT
SSAT
ISEE
PSAT
SAT
ACT
AP Exam
Science Tutoring
Physics Tutoring
Chemistry Tutoring
Biology Tutoring
Math Tutoring
Pre-Algebra Tutoring
Algebra Tutoring
Pre Calculus Tutoring
Calculus Tutoring
Geometry Tutoring
Trigonometry Tutoring
Statistics Tutoring
Quick links
Free Worksheets
Fact sheet
Sales Partner Opportunities
Parents
Passive Fundraising
Virtual Fundraising
Our Expert Tutors
Safe and Secure Tutoring
Interactive Online Tutoring
After School Tutoring
Elementary School Tutoring
Middle School Tutoring
High School Tutoring
Home Work Help
Math Tutors New York City
Press
©2022 eTutorWorld Terms of use Privacy Policy Site by Little Red Bird
©2022 eTutorWorld
Terms of use
Privacy Policy
Site by Little Red Bird







