Rational & Irrational Numbers Math Free Worksheet for Grade 8

Rational & Irrational Numbers Worksheet

Struggling to find quality practice questions and worksheets for “Rational & Irrational Numbers”?

eTutorWorld’s free worksheet is here to rack your brains and help you practice for your tests. You can go ahead and download this arithmetic worksheet from here.

The free worksheet covers a range of questions on addition, subtraction, and multiplication of Rational and irrational Numbers.

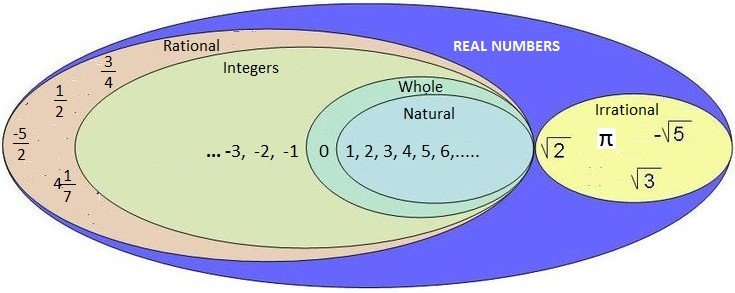
Rational Numbers

Any number that can be expressed in the form $\\frac{p}{{q}}$ where p, q are integers and q $\\neq$ 0 is called a rational number. p is called the numerator and q the denominator of the rational number.

Any integer can be expressed as a rational number. For example, 5 can be written as $\\frac{5}{1}$ in the rational form.

The numbers $\\frac{4}{-5}$ , $\\frac{6}{4}$ , $\\frac{-11}{-9}$ , $\\frac{8}{1}$ , $\\frac{-7}{-1}$ , $\\frac{0}{-3}$ ,… are all rational numbers

All fractions are rational numbers. All integers are also rational numbers. There are many rational numbers which are neither fractions nor integers.

Rational numbers can also be represented on the number line.

Irrational Numbers

All numbers which are not rational are called irrational numbers, which means all the numbers that cannot be put in the form $\\frac{p}{q}}$ where p, q are integers and q $\\neq$ 0 are called ‘irrational numbers’.

Any rational number will be a terminating decimal or a repeating decimal. For example, $\\frac{7}{8}}$ = 0.875(terminating decimal)

$\\frac{5}{12}$ = 0.41666…(repeating decimal)

An irrational number is a decimal that is neither terminating nor repeating.

The square roots of 2, 3, 5, 6, 7, 8 are all irrational numbers.

Frequently Asked Questions

What are rational numbers?

A rational number is any number that can be expressed as a fraction of two integers. For example, 3/4, -2/5, and 1 are all rational numbers.

What are irrational numbers?

Irrational numbers cannot be expressed as fractions of two integers. Examples include √2, π (pi), and e (Euler’s number).

Why are rational and irrational numbers important in math?

Understanding these types of numbers is fundamental to various mathematical concepts and real-world applications, from basic arithmetic to advanced calculus and geometry.

How can I identify rational and irrational numbers?

Rational numbers have repeating or terminating decimals, while irrational numbers have non-repeating, non-terminating decimals.

What is a Rational & Irrational Numbers Worksheet?

A Rational & Irrational Numbers Worksheet is an educational tool designed to practice and assess your knowledge of rational and irrational numbers in mathematics.

Who can benefit from using these worksheets?

These worksheets are suitable for students of various grade levels, teachers, and anyone looking to improve their understanding of these number types.

What topics are covered in a Rational & Irrational Numbers Worksheet?

These worksheets typically cover identifying rational and irrational numbers, performing operations with them, converting between fractions and decimals, and solving problems involving these numbers.